407685: GYM102873 E Count Substrings

You are given a string s consisting only of lowercase Latin letters. s has length $$$n$$$.

You are also given a string t made of $$$2$$$ lowercase Latin letters.

Your task is to count the number of pairs (L, R) such that the substring starting from L and ending in R (that is, $$$s_ls_{l+1}s_{l+2}... s_r$$$) contains t.

Note that the answer may not fit in 32-bit integer data types.

The first line contains a single integer $$$n$$$ $$$(1 \leq n \leq 2\cdot10^5)$$$- the length of string $$$s$$$.

The second line contains the string s.

The third line contains the string t of length $$$2$$$.

The number of pairs (L, R) such that the substring starting from L and ending in R contains t.

4
dabc
ab

4

8
hshshshs
hs

25

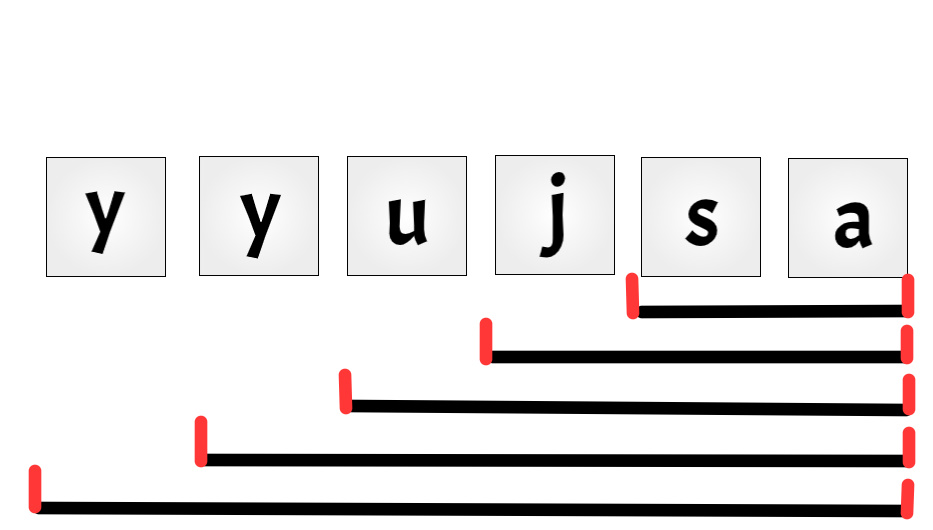
6
yyujsa
sa

5

5
fpmbe
ai

0

For the first test: s $$$=$$$ "dabc" and t $$$=$$$ "ab". So, all the pairs(L, R) are: (0, 2), (1, 2), (1, 3), (0, 3) corresponding to the substrings: "dab", "ab", "abc", "dabc".

For the second test, please note that, for example, each of four substrings "hs" is counted separately towards the answer, because we count pairs $$$[L, R]$$$ rather than distinct substrings.

For the third test, there are $$$5$$$ possible pairs and they are: