407704: GYM102878 F SVM

F. SVMtime limit per test3 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

Lancern is learning Support Vector Machine(SVM), a widely known linear classification model, recently. A set of data points(represent as high dimension points) are linear divisible if there exists a separating hyperplane which divides all data points into two parts, data points on the one side of the separating hyperplane all belong to one class, while data points on the other side all belong to the other class, and no data points are on the separating hyperplane. The SVM aims to find a separating hyperplane that satisfies the minimum Euclidean distance from any data point to the separating hyperplane is maximized. Those points with the minimum distance are called support vectors, and the distance between support vectors is called margin(also equals double minimum distance from support vector to the optimal separating hyperplane).

Poor Lancern doesn't understand SVM at all, neither do you, but the deadline of his assignment of SVM is coming, so Lancern asks you to help him solve his assignment.

In his assignment, all data points are given in 3-dimension real space, and each point only belongs to one of the two classes. You should help Lancern determine whether the data points are linear divisible? If they are, you have to calculate the margin.

Input

The first line contains one integer $$$n$$$ $$$\left(2\le n\le 500\right)$$$, indicating the number of data points.

The following $$$n$$$ lines, each line contains 4 integers $$$x_i$$$, $$$y_i$$$, $$$z_i$$$ $$$\left(\left|x_i\right|, \left|y_i\right|, \left|z_i\right|\le 1000\right)$$$ and $$$c_i$$$ $$$\left(c_i \in \left\{1, 2\right\}\right)$$$, denoting the coordinate of data point and its class.

It is guaranteed that no two data points have the same coordinate and each class has at least one data point.

Output

If the data points are linear divisible, output the margin. Otherwise, output -1 instead.

Your answer is considered correct if and only if $$$\frac{\left|a-b\right|}{\max\left(1, a\right)}\le 10^{-6}$$$, where $$$a$$$ is the jury's answer, $$$b$$$ is your output.

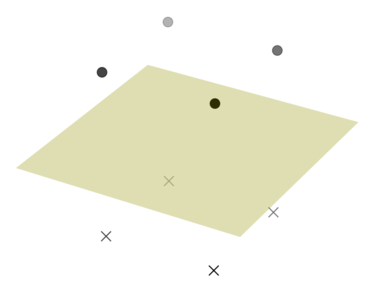
ExamplesInput

8
0 0 0 1
1 0 0 1
1 1 0 1
0 1 0 1
0 0 1 2
1 0 1 2
1 1 1 2
0 1 1 2

Output

1.00

Input

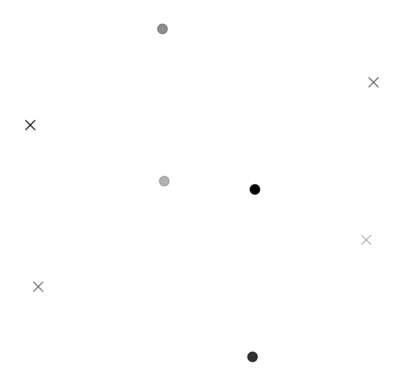
8
0 0 0 1
1 0 0 2
1 1 0 1
0 1 0 2
0 0 1 1
1 0 1 2
1 1 1 1
0 1 1 2

Output

-1

Note

In the first example, obviously, $$$z = 0.5$$$ is the optimal separating plane.

In the second example, the data points are not linear divisible.