407717: GYM102881 F Geometry?

Baby Ehab likes $$$xor$$$, but KEE likes geometry. That's why this next problem is a combination of both!

Given two lines having an integer power-of-2 slope each $$$s_1$$$ and $$$s_2$$$, and passing through the point $$$(0,0)$$$; along with an interval on the $$$x-axis$$$, find the value of the following summation:

Where $$$y_{1,i}$$$, $$$y_{2,i}$$$ are the $$$y-coordinates$$$ of the first and second line respectively for the $$$i_{th}$$$ integer $$$x-coordinate$$$ in the interval provided.

The first line contains an integer $$$T$$$ $$$(1 \leq T \leq 1000)$$$, the number of testcases.

Each testcase consists of one line containing $$$4$$$ integers $$$s_1,$$$ $$$s_2,$$$ $$$x_l,$$$ $$$x_r$$$ $$$(1 \leq s_1,$$$ $$$s_2 \leq 2^{20},$$$ $$$1 \leq x_1,$$$ $$$x_r \leq 10^{12})$$$ where $$$s_1,$$$ $$$s_2$$$ are the slopes of the lines and $$$x_l,$$$ $$$x_r$$$ are the boundaries of the interval on the x-axis. It's guaranteed that $$$s_1,$$$ $$$s_2$$$ are an integer powers-of-2 (i.e. $$$s = 2^k$$$ for some non-negative integer $$$k$$$).

For each testcase, output one line containing the sum of the $$$xor$$$ of the y-coordinates on both lines in the given interval. To avoid large numbers, output the sum modulo $$$1000000007$$$. The sum is calculated under the modulo; however, the xor at each individual sum is not.

3
1 2 1 4
4 8 3 7
128 1024 100000 125000

26
204
832054810

The first test:

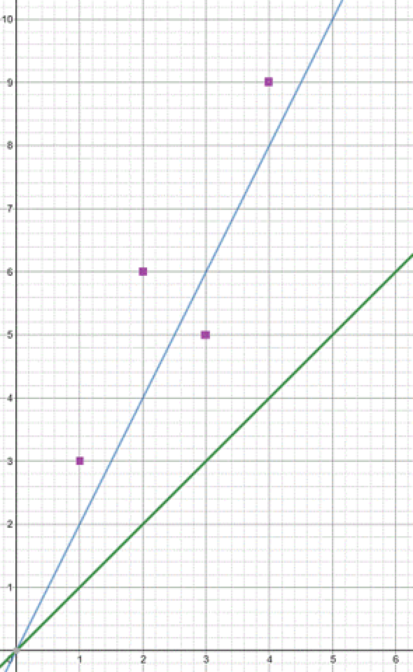
The squares denotes the xor at each point. $$$(1 \oplus 2) + (2 \oplus 4) + (3 \oplus 6) + (4 \oplus 8) = 3 + 6 + 5 + 12 = 26$$$.

It's recommended to use 64-bit integer types to avoid overflow.