407873: GYM102911 I Implementation Problem

Alice has encountered a puzzle room in a video game. To progress, she needs to slide some large cubes into their proper positions in order to activate a magic portal which leads deeper into the dungeon. The puzzle is also further complicated by large immovable obstacles and holes of different depths that are scattered throughout the room.

We can encode the contents of the room in a grid with $$$N$$$ rows and $$$M$$$ columns, and represent this grid with $$$N$$$ strings, each containing $$$M$$$ ASCII characters. The following are what each character corresponds to:

• . corresponds to open space.
• # corresponds to an immovable obstacle.
• An uppercase English letter from A to Z corresponds to a cube of a particular color. Two cubes have the same color if (and only if) they are represented by the same letter, and cubes of the same color are indistinguishable from one another. Underneath the initial position of each cube is open space.
• A single digit from 1 to 9 corresponds to a hole in the ground, with the numerical value of the digit indicating the capacity of that hole.
• The grid is implicitly surrounded by a wall of obstacles on all sides.

Alice can use magic to tilt the room in one of the four cardinal directions (north, south, east, or west). When she does so, the cubes move in the following manner,

• Each cube moves continuously in the indicated direction until it hits an obstacle, hits a wall (an edge of the grid), hits another cube which can no longer move, or enters a space with a hole with nonzero capacity.
• A cube that enters a space with a hole with nonzero capacity falls into that hole, and the capacity of the hole then decreases by $$$1$$$. A hole with capacity 0 acts functionally as open space from that point onwards.

Alice has a series of commands she wishes to execute. Each is described by a single direction, and involves tilting the room in the indicated direction until all cubes are no longer moving. A command can be represented by one of the characters N, S, E, or W, corresponding to the directions north, south, east, and west, respectively.

Alice gives you a string which contains all the commands she wishes to execute, in order from left to right. Output the state of the room after all her commands have been executed in the indicated order.

The first line of input contains two space-separated integers $$$N$$$ and $$$M$$$, the number of rows and the number of columns in the grid.

The next $$$N$$$ lines of input contain a string with $$$M$$$ characters. The $$$j$$$th character of the $$$i$$$th string corresponds to the space in the $$$j$$$th column of the $$$i$$$th row of the grid, as described in the problem statement.

This is followed by a single line containing a single string which describes the commands that Alice wishes to perform.

Output $$$N$$$ lines, each containing a string with $$$M$$$ characters, representing the state of the room after all of Alice's commands, in the same format as it is given in the input. If a cube ultimately occupies some space, output the color of that cube. Otherwise, output the open space, obstacle, or hole, in the same format as in the input. We point out that after all the commands, it may be possible to have a hole with capacity $$$0$$$, which we represent with the character 0.

$$$1 \leq N, M \leq 20$$$

Alice gives at least $$$1$$$ and at most $$$200$$$ commands.

Subtask 1 (15 points):

There are no holes or obstacles in the room.

Subtask 2 (15 points):

There are no holes in the room.

Subtask 3 (15 points):

Only S (south) commands will be given.

Subtask 4 (15 points):

Only S and N (south and north) commands will be given.

Subtask 5 (15 points):

Only S and E (south and east) commands will be given.

Subtask 6 (15 points):

Alice gives at most $$$10$$$ commands.

Subtask 7 (10 points):

No further constraints.

4 5
ACD..
B#...
.E#..
#....
S

.C...
A#D..
B.#..
#E...

4 5
ACD..
B#...
.E#..
#....
SE

....C
A#..D
.B#..
#...E

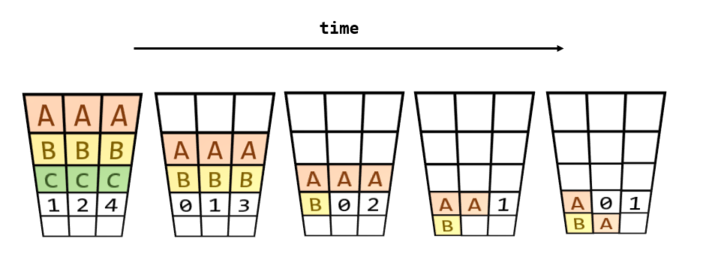
5 3
AAA
BBB
CCC
124
...
S

...
...
...
A01
BA.

In the first sample test case, we tilt the room so that all the cubes slide south.

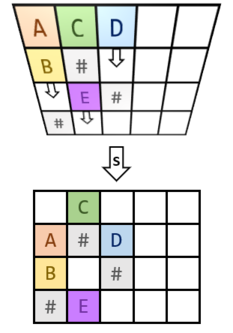
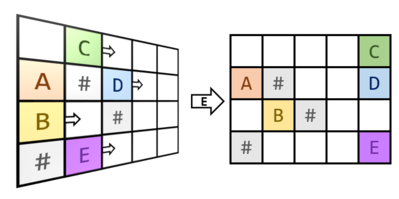
In the second sample test case, first we make all the cubes slide south, just like in the first sample. Then, the next command is to tilt the room so all cubes slide east.

For the third sample test case, the diagram below shows the step-by-step process of the cubes sliding southwards and into the holes with various capacities.

The hole in the first column becomes fully filled, and is covered in the final state by the A cube over it. The hole in the second column becomes fully filled, and we can see its 0 in the final state; the A cube slides over it and rests at the bottom of the grid. The hole in the third column has all three cubes in its column slide into it, and it still has a capacity of 1 after that.