408215: GYM103055 I Grammy and Ropes

The original problem name is "Separation Judgement Problem of Rope-made 3 Cycle Venn Diagram with Overlapping Intersections", but it can't fit into the margin.

Three cyclic ropes are lying on the table, the projection of which forms a Venn Diagram.

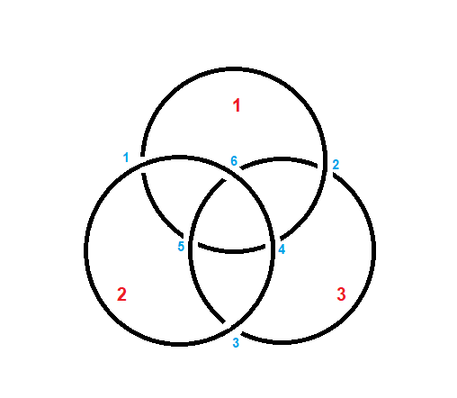
As the illustration shows, these ropes (indexed from one to three) have six overlapping intersections, indexed from one to six respectively.

Grammy wants to pull the ropes apart, but it seems that they are tied together, so she needs to cut a subset of the three ropes with scissors. She is wondering how many different ways are there to choose the subset so that these ropes are separable afterward. Can you tell her the answer?

Note: Two subsets are different if and only if there is at least one rope being chosen in one of the subsets and not being chosen in the other. The empty set should also be considered.

The input contains only a single case.

The only line of the input consists of $$$6$$$ boolean variables (either "true" or "false") in one line, the $$$i$$$-th one representing whether the larger-indexed rope is on top of the other or not at the $$$i$$$-th intersection.

One integer, the answer to the problem.

true false false true true false

6