408400: GYM103114 D Dllllan and his friends
Description
Do you know why lllllan is called "Su Mama"? If you don't know, I'll tell you now. Because lllllan is very friendly to his friends. Every year when he returns to his hometown after one year's study, he will visit every friend once. It can be seen that he really attaches great importance to the relationship between him and his friends, and when they are in trouble, lllllan will always give a hand. I'm lucky to be one of these friends.
As usual, lllllan is going to visit his friends. But the difference is that lllllan is moveing house this year. Considering that his former house is far away from some friends' houses, so he wanted the new house to be the same distance from all his friends' houses.Now, lllllan wants to visit all his friends from his home.You know, lllllan has a kind of magic, he can change the length of the road he walked to $$$0$$$. Now you need to find the location of lllllan's new house, and the minimum distance after lllan visited all his friends.To simplify this problem, we assume that lllllan's hometown is in a Cartesian coordinate system, and each house is regarded as a point on the plane.
The coordinates of each point (including lllllan's home) are integers.
InputThe first line of input contains one integer $$$n$$$, where $$$n(3 \leq n \leq 10^6)$$$ is number of lllllan's friends.
The next $$$n$$$ lines describe the house of lllllan's friends, the $$$i$$$-th of which contains two integers $$$x_i,y_i (1 \leq x_i, y_i \leq 10^4)$$$, which are the coordinates of the $$$i$$$-th houses.
The testcase ensures that all coordinates are different.
OutputIn the first line, output the coordinates of the points meeting the conditions, separated by spaces.
The second line outputs a number, the minimum distance.
Formally, let your answer be $$$a$$$, and the jury's answer be $$$b$$$. You answer is accepted if and only if $$$\frac{|a-b|}{max(1,|b|)} \leq 10^{-4}$$$.
If there is no coordinate of the point that meets the condition, output "-1"(without quotes) in one line.
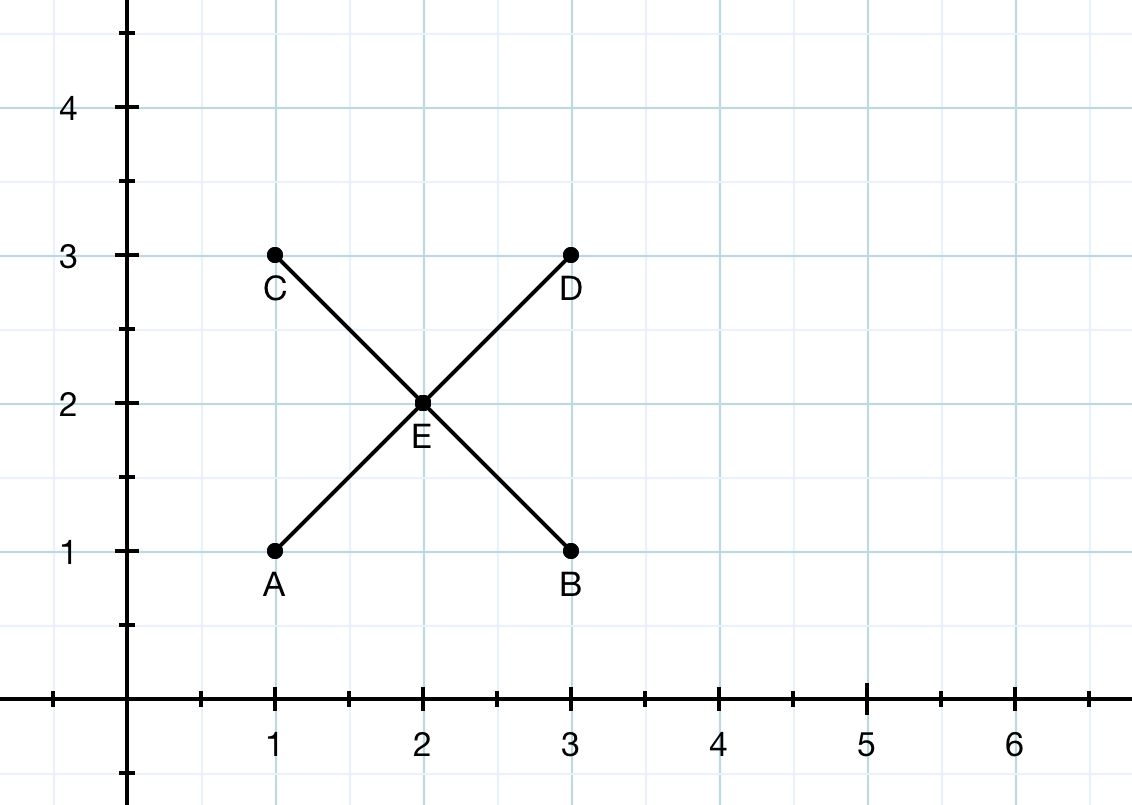
ExamplesInput4 1 1 1 3 3 1 3 3Output
2 2 5.6568542495Input
5 3 1 2 3 3 5 4 4 6 5Output
-1Note
The situation in the first example: