408485: GYM103149 C Angry Cows

Recent years have seen a rapid spread of the Extremely Green Oxen Illness (EGOI), which is a disease that makes cows dangerous to hikers. After several incidents it has been decided that we need to separate the areas where cows graze from the part of Alps where people want to hike.

You are given a map of the Alps. On the map there are $$$n$$$ areas. Each of them can be either a cow-populated area, a hiking area, or an unused area. Some pairs of areas are connected by bidirectional trails. Each trail has a non-negative length. (In graph-theoretic terms, the map is an undirected graph with weighted edges.)

You can build walls in some of the areas. Once you build a wall in an area, the area becomes inaccessible to hikers and cows – they will no longer be able to walk through such an area.

Your task is to select the set of areas where walls will be placed. This set of areas must satisfy the following conditions:

• It must consist only of unused areas.
• It must separate cow-populated areas from hiking areas. That is, a cow should no longer be able to walk along trails from a cow-populated area to a hiking area (without passing through an area with a wall).
• It must not separate any hiking areas from each other. That is, a hiker should still be able to walk along trails from any hiking area to any other hiking area (without passing through an area with a wall).

If there are multiple ways to reach the above goal, we will care about the ease of maintenance of the walls. The walls will be maintained by specialized crews. There is one such crew based in each hiking area.

For any area $$$A$$$ we define its remoteness as the minimum length of a path of trails between $$$A$$$ and some hiking area. (The length of a path is the sum of the lengths of its trails. Note that these paths may pass through walls and cow-populated areas – the wall maintenance crew has all the skills and equipment needed to do that.)

The remoteness of a set of areas is then the maximum remoteness of any area in this set.

Among all sets of areas with walls that have the required properties, find and return one with the smallest possible remoteness. If there are many such sets of areas, you may return any one of them.

Note that the number of areas does not matter. In particular, it is not required to use as few walls as possible.

The first line of the input contains two space-separated integers $$$n$$$ and $$$m$$$ ($$$2 \leq n \leq 3 \cdot 10^5$$$, $$$n-1 \leq m \leq 3 \cdot 10^5$$$) – the number of areas and trails, respectively. The areas are numbered from $$$1$$$ to $$$n$$$.

The second line contains $$$n$$$ space-separated integers $$$t_1, ..., t_n$$$, where $$$t_i$$$ is $$$-1$$$ if the $$$i$$$-th area is cow-populated, $$$0$$$ if it is unused, and $$$1$$$ if it is a hiking area.

The remaining $$$m$$$ lines describe trails. The $$$j$$$-th of them contains three space-separated integers $$$a_j$$$, $$$b_j$$$ and $$$\ell_j$$$ ($$$1 \le a_j < b_j \le n$$$, $$$0 \le \ell_j \le 10^9$$$), denoting a trail between areas $$$a_j$$$ and $$$b_j$$$ of length $$$\ell_j$$$.

It is guaranteed that:

• between any two areas there is at most one trail,
• it is currently possible to walk between any two areas using zero or more trails,
• there is at least one cow-populated area,
• there is at least one hiking area.

If it is impossible to build the walls according to the requirements, output -1.

Otherwise, the first line of the output should contain an integer $$$k$$$ – the number of walls you want to build. The second line should contain $$$k$$$ integers – the numbers of areas where you want to build the walls. (These numbers must be distinct numbers between $$$1$$$ and $$$n$$$, inclusive. They do not have to be in any particular order.)

The output will be accepted if it is an allowed set of walls with minimum remoteness.

Subtask 1 (7 points): $$$n \le 10$$$.

Subtask 2 (22 points): all lengths $$$\ell_j = 0$$$.

Subtask 3 (16 points): there is exactly one hiking area.

Subtask 4 (11 points): there are exactly $$$n-1$$$ trails (in graph-theoretic terms, the graph is a tree).

Subtask 5 (8 points): we have $$$n, m \le 2000$$$ and all lengths $$$\ell_j = 1$$$.

Subtask 6 (36 points): there are no additional constraints.

10 14
1 0 1 0 0 0 0 0 -1 -1
1 2 1
1 6 1
2 3 1
2 5 2
3 4 1
4 5 1
4 8 2
5 6 1
5 7 1
6 7 2
6 10 1
7 8 1
7 9 1
8 9 1

3
4 5 6 

5 5
1 0 0 -1 0
1 2 1000
2 3 1000
3 4 10
4 5 10
1 5 10

2
3 5 

4 3
1 0 -1 1
1 2 0
2 3 21
2 4 13

-1

In all of the figures, blue (dotted) is used for hiking areas, brown (full) for cow-populated areas and orange (dashed) for walls.

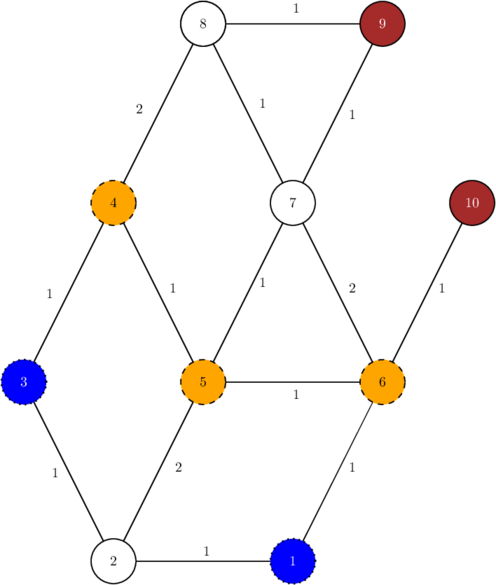
In the first example, the minimum possible remoteness is 2, achieved by placing walls in areas $$$4$$$, $$$5$$$ and $$$6$$$. Note that one cannot place walls in areas $$$4$$$, $$$2$$$ and $$$6$$$, even though this would yield a remoteness of $$$1$$$, because then it would be impossible to travel between the hiking areas $$$1$$$ and $$$3$$$ without passing through a wall.

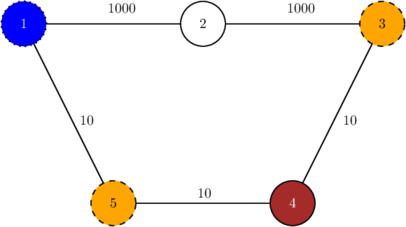
In the second example, the remoteness of area 2 is 1000, and the remoteness of area 3 is 30, as it can be reached via path 1–5–4–3. (Recall that maintenance crews can pass through walls and cow-populated areas.) Therefore we should place walls in areas 5 and 3 (not 2), and the remoteness will be 30.