408649: GYM103241 X Endeavor's Agency
Description
Endeavor is a great hero and wants to help keep his country, Japan, safe. Japan contains $$$N$$$ $$$(1 \leq N \leq 10^5)$$$ cities numbered from $$$1$$$ to $$$N$$$. There are also $$$M$$$ $$$(0 \leq M \leq 5 \cdot 10^5)$$$ bidirectional roads where the $$$i$$$th connects city $$$M_{i,a}$$$ to city $$$M_{i,b} \, (M_{i,a} \neq M_{i,b})$$$ and makes the two cities neighbors. It is guaranteed that there is at most $$$1$$$ road between any pair of cities. Japan also has a peculiar feature. Consider a path that visits $$$w$$$ cities from city $$$u$$$ to city $$$v$$$, where the $$$i$$$th city on the path is $$$p_i$$$. Then if $$$p_i < p_{i+1}$$$ for all $$$i<w$$$, city $$$u$$$ and city $$$v$$$ are neighbors.
Endeavor decides to build a hero office in some cities. To ensure safety and efficiency, he wants at least one of the conditions to be satisfied for every city:
The city has no neighbors.
The city contains an office.
All neighbors of the city contain an office.
Japan is considered safe if this requirement is met.
Unfortunately, as great of a hero as Endeavor is, he still hasn't defeated the greatest villain—money! To cut down on costs, Endeavor's agency decides to build the minimal number of offices such that Japan is safe. Currently, Endeavor is busy roasting evildoers (literally), so he wants you to find this out for him.

The first line contains one integer, $$$T$$$ $$$(1 \leq T \leq 10^5)$$$, the number of test cases. Then $$$T$$$ test cases follow.
The first line of each test case contains $$$2$$$ integers, $$$N, M$$$.
The next $$$M$$$ lines of each test case contain $$$2$$$ integers. The $$$i$$$th such line contains $$$M_{i,a}, M_{i,b}$$$.
It is guaranteed that the sum of $$$N$$$ over all test cases does not exceed $$$10^5$$$. It is also guaranteed that the sum of $$$M$$$ over all test cases does not exceed $$$5 \cdot 10^5$$$.
OutputFor each test case, output the minimal number of offices to build such that Japan is safe.
ExampleInput3 1 0 3 1 2 3 4 3 3 1 4 2 2 3Output
0 1 2Note
Here's the country from first test case:

Here's the country from second test case:
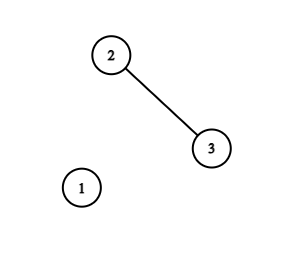
In the second test case, there are $$$3$$$ cities and $$$1$$$ road. A road connects city $$$2$$$ to city $$$3$$$. To minimize the offices built, Endeavor can build an office in either city $$$2$$$ or city $$$3$$$. The answer is $$$1$$$.
Here's the country from third test case:
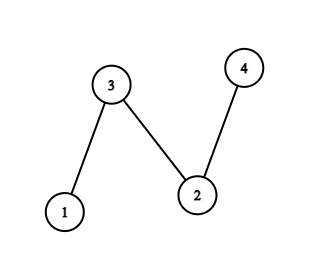
In the third test case, there are $$$4$$$ cities and $$$3$$$ roads. There is a road that connects city $$$3$$$ to city $$$1$$$, a road that connects city $$$4$$$ to city $$$2$$$, and a road that connects city $$$2$$$ to city $$$3$$$. To minimize the offices built, one solution is for Endeavor to build an office in city $$$1$$$ and city $$$2$$$. Of course, building offices in cities $$$(1,2), \, (3,2),$$$ or $$$(3,4)$$$ all work to achieve the minimal number of offices. The answer is $$$2$$$.
Problem idea: codicon
Problem preparation: codicon
Occurances: Advanced 12