408886: GYM103372 A Histogram Sequence 3
Description
Consider the histogram composed of $$$n$$$ squares with side lengths $$$a_1, a_2, \cdots, a_n$$$. Let's call the sequence $$$(a_1, a_2, \cdots, a_n)$$$ the histogram sequence of this histogram.
Let's consider the height of each column in this histogram. The first $$$a_1$$$ columns will each have height $$$a_1$$$, the following $$$a_2$$$ columns will each have height $$$a_2$$$, ... and the last $$$a_n$$$ columns will each have height $$$a_n$$$. Now, let us define the height sequence $$$(b_1, b_2, \cdots, b_{a_1 + a_2 + \cdots + a_n})$$$ where $$$b_j\ (1 \le j \le a_1+a_2+\cdots+a_n)$$$ is the height of the $$$j$$$-th column.
For example, the histogram with $$$(3, 2, 1, 4)$$$ as its histogram sequence has $$$(3, 3, 3, 2, 2, 1, 4, 4, 4, 4)$$$ as its height sequence.
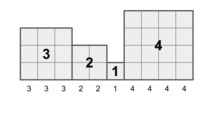
Write a program to find the histogram sequence given the height sequence.
InputThe first line contains a single integer $$$m\ (1 \le m \le 10^6)$$$ representing the length of the height sequence $$$\{b_i\}$$$ is given.
The second line of the input contains $$$m$$$ integers, the height sequence. Specifically, the $$$i$$$-th integer in the line is $$$b_i\ (1 \le b_i \le m)$$$.
The input is designed such that the provided height sequence corresponds to a valid histogram sequence.
OutputOutput $$$n$$$ integers on a single line, $$$a_1, a_2, \cdots, a_n$$$ where $$$(a_1, a_2, \cdots, a_n)$$$ is the histogram sequence corresponding to the given height sequence. If there are multiple answers, any one of them will be accepted.
ExamplesInput10 3 3 3 2 2 1 4 4 4 4Output
3 2 1 4Input
5 2 2 2 2 1Output
2 2 1