409143: GYM103446 H Life is a Game

Life is a game.

The world can be regarded as an undirected connected graph of $$$n$$$ cities and $$$m$$$ undirected roads between the cities. Now you, the life game player, are going to play the life game on the world graph.

Initially, you are at the $$$x$$$-th city and of $$$k$$$ social ability points. You can earn social ability points by living and working. Specifically, you can earn $$$a_i$$$ social ability points by living and working in the $$$i$$$-th city. But in this problem, you cannot earn social ability points duplicatedly in one city, so you want to travel the world and earn more social ability points. However, the roads are not easy. Specifically, there is an ability threshold $$$w_i$$$ for the $$$i$$$-th road, you should be of at least $$$w_i$$$ social ability points to go through the road. Moreover, Your social ability point will not decrease when passing roads but just need to be at least $$$w_i$$$ if you want to go through the $$$i$$$-th road.

So as you can see, the life game is just living, working and traveling repeatedly. There are $$$q$$$ game saves. For each game save, the initial city and social ability point is given and the player has not lived or worked in any city. Now you, the real life game player, need to determine the maximum possible number of social ability points you can have in the end of the game and output it for each given game save.

The first line contains three integers $$$n,m,q\,(1\le n,m,q \le 10^5)$$$, denoting the number of cities, roads and game saves respectively.

The second line contains $$$n$$$ integers $$$a_1, a_2, \cdots, a_n\,(1\le a_i \le 10^4)$$$, denoting the bonus social ability points for the cities.

Following $$$m$$$ lines each contains three integers $$$u, v, w\,(1\le u < v \le n, 1\le w \le 10^9)$$$, denoting that cities $$$u,v$$$ are undirectedly connected by a road of ability threshold $$$w$$$.

Following $$$q$$$ lines each contains two integers $$$x, k\,(1\le x \le n, 1\le k \le 10^9)$$$, denoting the game saves.

For each game save, output one line containing one integer, denoting the maximum possible number of social ability points you can have.

8 10 2
3 1 4 1 5 9 2 6
1 2 7
1 3 11
2 3 13
3 4 1
3 6 31415926
4 5 27182818
5 6 1
5 7 23333
5 8 55555
7 8 37
1 7
8 30

16
36

Following is a illustration of the given graph.

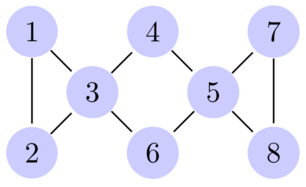
• For the first game save, you can reach 4 cities $$$\{1,2,3,4\}$$$ and have $$$7+3+1+4+1 = 16$$$ social ability points in the end
• For the second game save, you can only reach the initial city $$$\{8\}$$$ and have $$$30+6 = 36$$$ social ability points in the end