409240: GYM103466 C Digital Path

C. Digital Pathtime limit per test1 secondmemory limit per test512 megabytesinputstandard inputoutputstandard output

Zhe the bully, is condemned by all kinds of evil, like bullying those who are weaker. His teammates have been mistreated for a long time. Finally, they decided not to put up with their buddy any more and flee to Digital Village, with the bully in hot pursuit. Due to difficult terrain and a considerable amount of Digital Paths staggered, they can't be easily arrested.

Getting familiar with the terrain as soon as possible is important for these innocents to escape the threat of bullying. All they need now is to count the number of Digital Paths in Digital Village.

To simplify the problem, Digital Village is abstracted into a grid with $$$n$$$ rows and $$$m$$$ columns filled by integers. A Digital Path is a continuous walk in the grid satisfying the following conditions:

• adjacent boxes in the walk share a common edge;
• the walk is maximal, which cannot be extended;
• the walk contains at least four boxes;
• going from one end to the other, the increment of values for any two adjacent boxes is exactly one.

Here we have some examples.

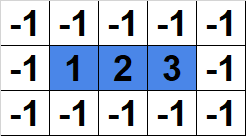
Figure 1: An invalid path.

The path in Figure 1 is invalid because its length is less than $$$4$$$.

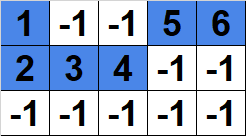
Figure 2: An invalid path.

The path in Figure 2 is invalid because it is not continuous.

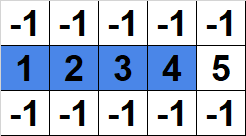
Figure 3: An invalid path.

The path in Figure 3 is invalid because it can be extended further.

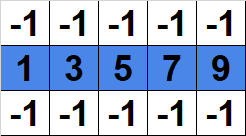
Figure 4: An invalid path.

The path in Figure 4 is also invalid because values in the path are not strictly increased by one.

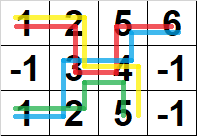
Figure 5: All valid paths.

Digital Paths may partially overlap. In Figure 5, there are $$$4$$$ Digital Paths marked by different colours.

Input

The first line contains two positive integers $$$n$$$ and $$$m~(1\le n,m\le 1\,000)$$$ describing the size of the grid.

Each of the next $$$n$$$ lines contains $$$m$$$ integers, the $$$j$$$-th of which, denoted by $$$a_{i,j}~(-10^7\le a_{i,j}\le 10^7)$$$, represents the value of the box in the $$$i$$$-th row and the $$$j$$$-th column.

Output

Output the number of Digital Paths modulo $$$(10^9+7)$$$.

ExamplesInput

3 5
1 2 3 8 7
-1 -1 4 5 6
1 2 3 8 7

Output

4

Input

4 4
1 2 3 4
2 3 4 3
3 4 3 2
4 3 2 1

Output

16