409267: GYM103470 F Paimon Polygon

Paimon just puts $$$(n+1)$$$ distinct points on the plane, one of which is a special point $$$O=(0,0)$$$, and denote the group of remaining points as $$$\mathbb{S}$$$.

We call a point set $$$\mathbb{U}$$$ strict convex set, if and only if $$$|\mathbb{U}| \ge 3$$$ and all the points from $$$\mathbb{U}$$$ lie exactly on the convex hull built from $$$\mathbb{U}$$$, with no three points lying on the same line.

You should divide $$$\mathbb{S}$$$ into two sets $$$\mathbb{A}$$$ and $$$\mathbb{B}$$$ so that:

• $$$\mathbb{A} \cap \mathbb{B}=\emptyset$$$.
• $$$\mathbb{A} \cup \mathbb{B}=\mathbb{S}$$$.
• $$$|\mathbb{A}| \ge 2, |\mathbb{B}| \ge 2$$$.
• The point set $$$\mathbb{A} \cup \{O\}$$$ is a strict convex set, and denote its convex hull as $$$C_{\mathbb{A} \cup \{O\}}$$$.
• The point set $$$\mathbb{B} \cup \{O\}$$$ is a strict convex set, and denote its convex hull as $$$C_{\mathbb{B} \cup \{O\}}$$$.
• The outlines(edges) of $$$C_{\mathbb{A} \cup \{O\}}$$$ and $$$C_{\mathbb{B} \cup \{O\}}$$$ only intersect at point $$$O$$$. That is, only one point $$$O$$$ satisfies that it lies both on the outlines of $$$C_{\mathbb{A} \cup \{O\}}$$$ and $$$C_{\mathbb{B} \cup \{O\}}$$$.

Please help Paimon to maximize the sum of the perimeters of these two convex hulls. That is, find a valid division $$$\mathbb{A}$$$ and $$$\mathbb{B}$$$ which maximizes $$$(L(C_{\mathbb{A} \cup \{O\}}) + L(C_{\mathbb{B} \cup \{O\}}))$$$, where $$$L(\text{polygon})$$$ means the perimeter of that polygon.

There are multiple test cases. The first line of the input contains an integer $$$T$$$ indicating the number of test cases. For each test case:

The first line contains one integer $$$n$$$ ($$$4 \le n \le 5 \times 10^5$$$) indicating the number of points in $$$\mathbb{S}$$$.

For the following $$$n$$$ lines, the $$$i$$$-th line contains two integers $$$x_i$$$ and $$$y_i$$$ ($$$-10^9 \le x_i, y_i \le 10^9$$$, $$$(x_i, y_i) \ne (0, 0)$$$) indicating the location of the $$$i$$$-th point in $$$\mathbb{S}$$$.

It's guaranteed that the points given in the same test case are pairwise different. However, there may be three points lying on the same line.

It's also guaranteed that the sum of $$$n$$$ of all test cases will not exceed $$$10^6$$$.

For each test case output one line containing a number indicating the maximum total perimeter. If there does not exist a valid division output "0" (without quotes) instead.

Your answer will be accepted if the relative or absolute error is less than $$$10^{-6}$$$.

3
4
0 3
3 0
2 3
3 2
5
4 0
5 -5
-4 -2
1 -2
-5 -2
4
0 1
1 0
0 2
1 1

17.2111025509
36.6326947621
0.0000000000

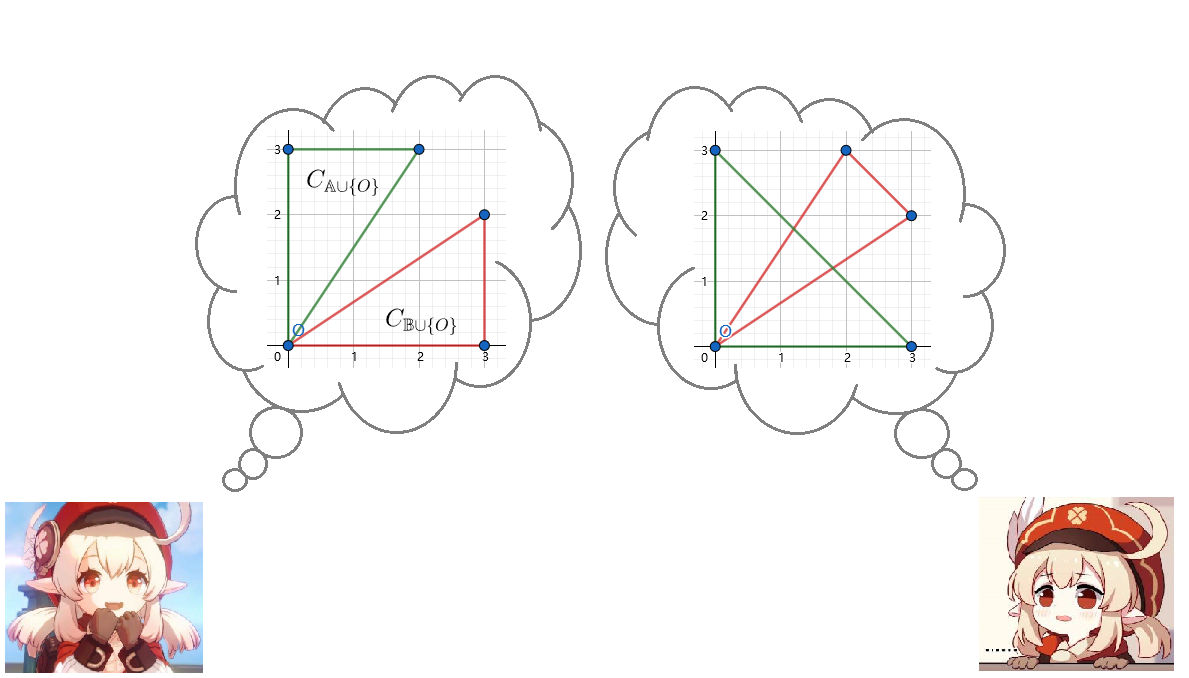
A valid division (left) and an invalid division (right) of the first sample test case are shown below.