409317: GYM103483 K Railroad sorting

Arsenii works as an operator at a sorting station, the scheme of which is shown on the image.

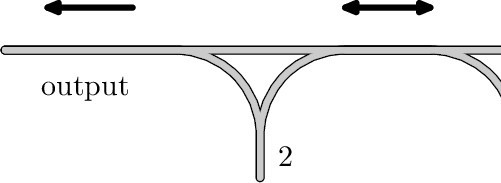
The station has an input track, an output track and two dead ends. The operator can move cars between tracks and dead ends.

If car $$$x$$$ is the first car on the input track, this car can be moved to any dead end. Command "1" moves the car to the dead end $$$1$$$, and command "2" moves car to the dead end $$$2$$$.

If the car $$$x$$$ is the closest car to the exit in one of the dead ends, it can be moved to output track. Command "-1" moves the car from the dead end $$$1$$$, and command "-2" moves the car from the dead end $$$2$$$.

Finally, you can move cars between dead ends. If $$$x$$$ is the closest car to the exit in one of the dead ends, it can be moved to another dead end. Command "12" moves the car from the dead end $$$1$$$ to the dead end $$$2$$$, and the command "21" moves the car from the dead end $$$2$$$ to the dead end $$$1$$$.

Please note that cars cannot be returned to a dead end from the output track and cannot be returned from a dead end to the input track. Also, you cannot move the car directly from the input track to the output track, it is required to use a dead end. Both dead ends can contain any number of cars.

A train of $$$n$$$ cars arrives on the input track, each car has a unique number from $$$1$$$ to $$$n$$$.

Arsenii must sort the cars so that they are all on the output track and their numbers from left to right are in ascending order. Help him form a sequence of commands that will help him to achieve this. The number of commands in the sequence must not be exceed $$$2 \cdot 10^6$$$.

The first line of input contains integer $$$n$$$ — the number of cars ($$$1 \le n \le 1000$$$).

The second line contains $$$n$$$ different integers $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \le a_i \le n$$$) — the numbers on the cars in order from left to right on the input track.

Print the sequence of commands that will cause the cars to be on the output track, and their numbers would be in ascending order. The sequence must contain no more than $$$2 \cdot 10^6$$$ command.

If there are multiple correct sequences, you can output any of them.

It is guaranteed that for any input data there is a sequence of commands containing at most $$$2 \cdot 10^6$$$ commands.

5
3 1 5 2 4

1
1
-1
1
1
-1
12
-1
1
-1
-2