409319: GYM103485 A Trying to Impress Cleopatra

Much is said about this great character of antiquity: Cleopatra. For example, it is said that she was highly educated and could make men completely fall in love with her. According to history, she got involved, for example, with the powerful Julius Caesar and Mark Antony.

However, if it is true that she could seduce, it is also said that many wanted to seduce her too. So, in the early days of the circus in Alexandria, an artist decided to try to impress Cleopatra with his performance, and thus try to seduce her. But to do that, he wants your help.

His presentation consists of moving with something like a bike/monocycle (were they really newly invented?!) inside and around an object with the shape of a convex polygon. More precisely, the artist chooses a side of the structure to be in contact with the ground and to serve as a base, and then he starts moving, inside the object, from left to right from the left vertex of the side chosen as the base. To impress Cleopatra, he wants to move through the structure without falling. So, to minimize the chances of this happening, he moves through the structure to the first vertex in which the next side forms $$$90^{\circ}$$$ or more with the floor; when this occurs, he stops. Also, he wants to move as much as possible inside the structure.

Therefore, to decide which side will be used as the base of the object and the starting place of the movement in his act, the artist wants to know the distance traveled considering the start of the movement on each of the $$$n$$$ sides of the structure.

The first line contains the integer $$$n$$$ — the number of points of the structure in format of a convex polygon.

The $$$i$$$-th of the next $$$n$$$ lines contains two integers $$$x_i$$$ and $$$y_i$$$, denoting the $$$i$$$-th vertex of the structure.

It is guaranteed that the points are given in counterclockwise order.

Constraints

• $$$n \leq 10^{5}$$$ and
• $$$0 \leq x_i, y_i \leq 10^9$$$.

For each vertex $$$i$$$, print the total distance covered by the artist when he leaves that vertex and moves counterclockwise in the structure until he stops.

The absolute or relative error should not exceed $$$10^{-6}$$$. Formally, for a fixed vertex, let your answer be $$$a$$$ , and the jury's answer be $$$b$$$. Your answer is accepted for this vertex if and only if $$$\frac{|a - b|}{\max (1, b)} \leq 10^{-6}$$$.

3
1 0
2 0
3 1

2.41421356
1.41421356
2.23606798

4
0 0
1 0
1 1
0 1

1.00000000
1.00000000
1.00000000
1.00000000

Each angle is the counterclockwise angle from ground to the chosen side. A polygon is convex if all their internal angles are less than or equal to $$$180^{\circ}$$$.

Consider the following three images to interpret the first example.

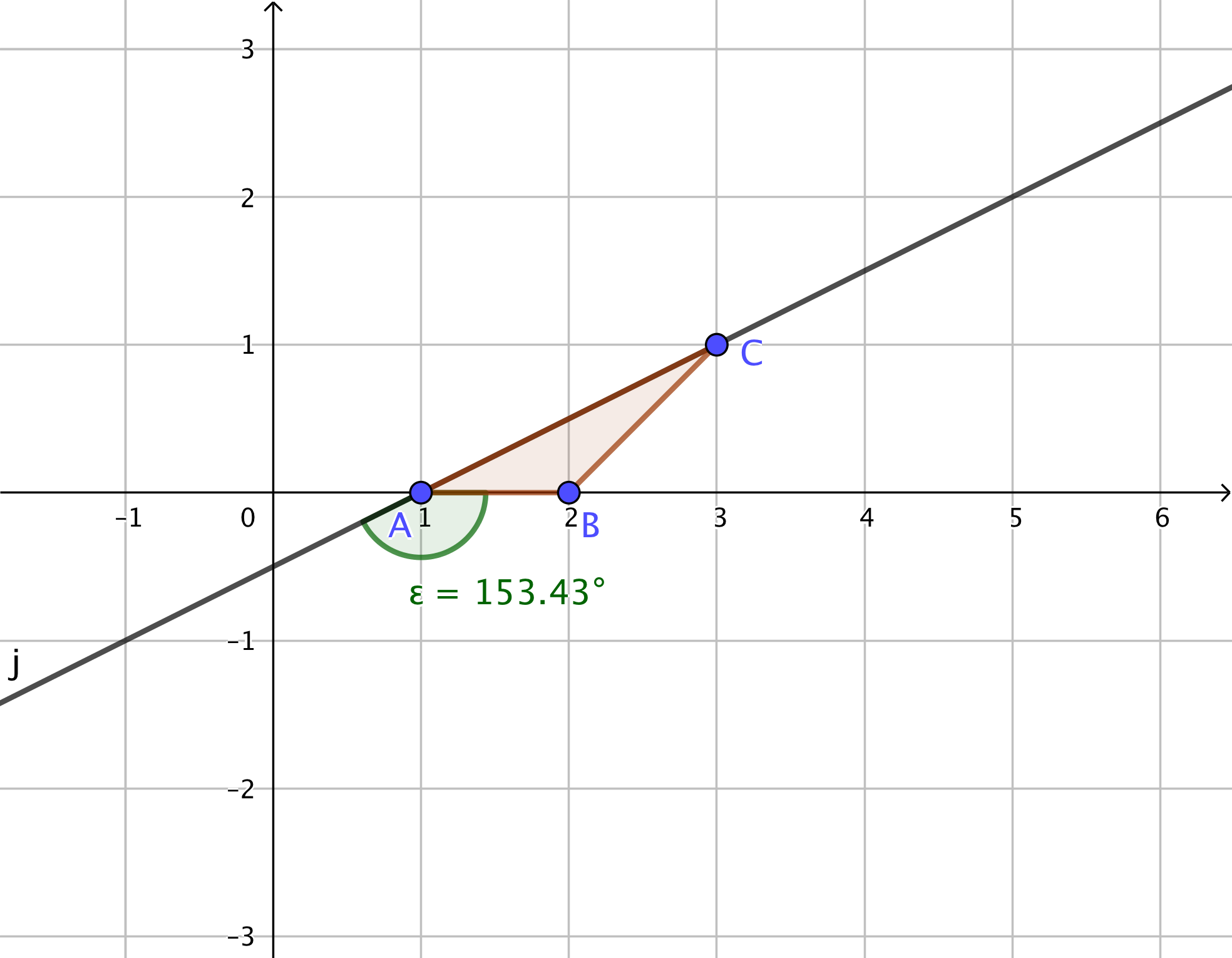
In the first image, consider the line $$$g$$$ to be the ground. The artist starts his movement on point $$$A$$$ and moves through the sides $$$AB$$$ and $$$BC$$$ stopping on the point $$$C$$$ since the angle between the side $$$CA$$$ and the ground is $$$\beta = 206.57^{\circ} \geq 90^{\circ}$$$. Thus, he traveled $$$|AB| + |BC| = 1 + \sqrt{2}$$$ on total.

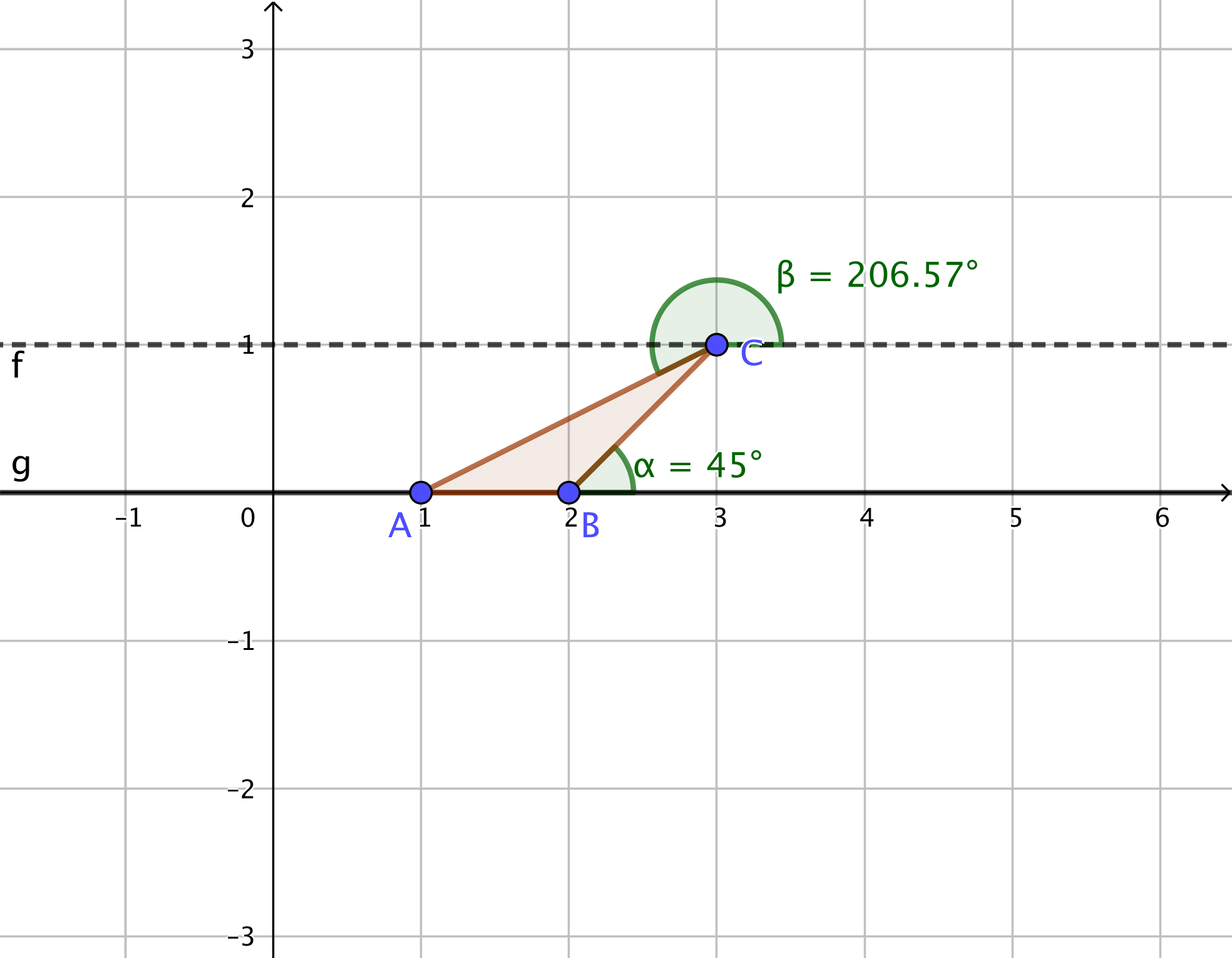
In the second image, consider the line $$$h$$$ to be the ground. The artist starts his movement on point $$$B$$$ and moves through the side $$$BC$$$ stopping on the point $$$C$$$ since the angle between the side $$$CA$$$ and the ground is $$$\gamma = 161.57^{\circ} \geq 90^{\circ}$$$. Thus, he traveled $$$|BC| = \sqrt{2}$$$ on total.

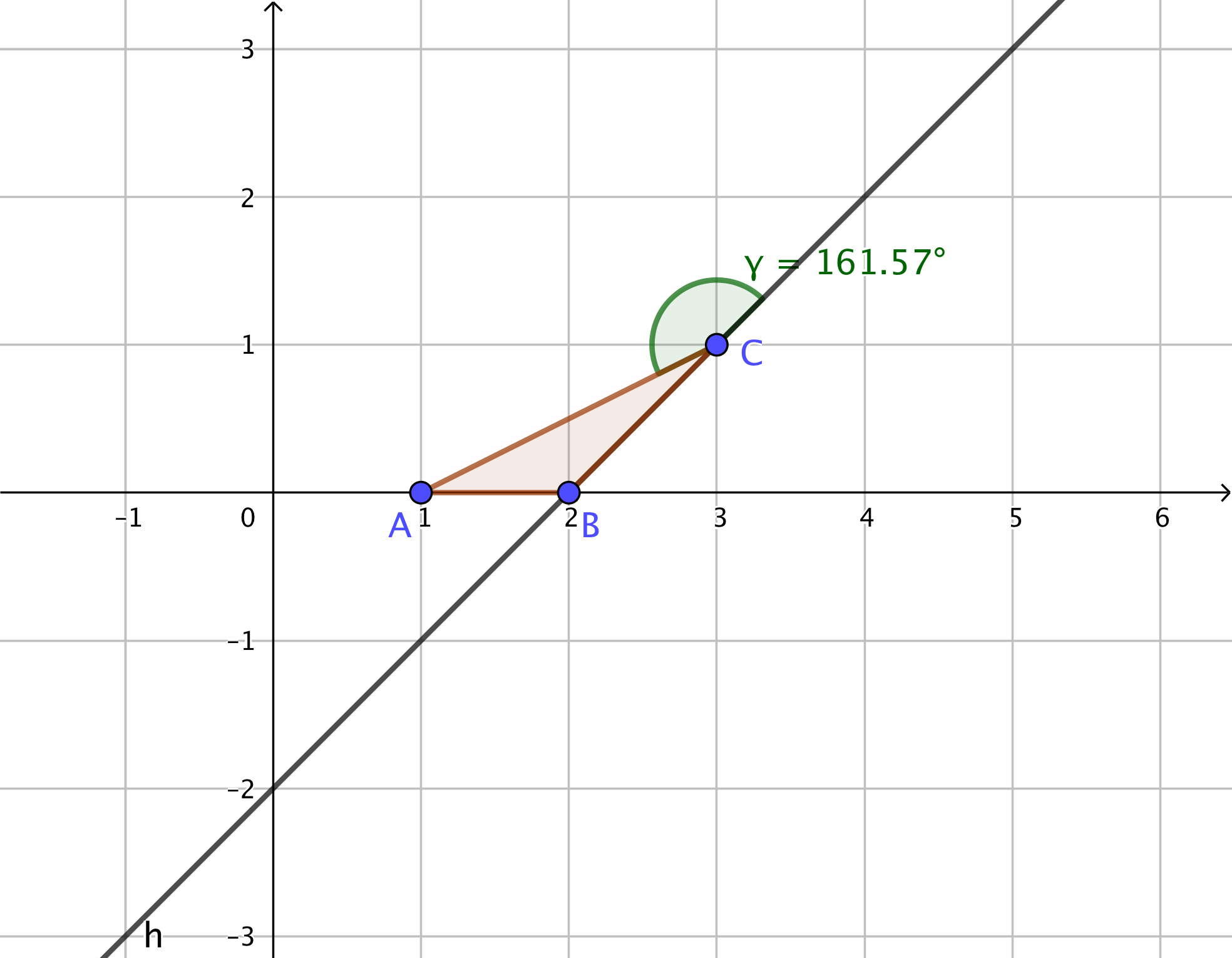
Finally, in the third image, consider the line $$$j$$$ to be the ground. The artist starts his movement on point $$$C$$$ and moves through the side $$$CA$$$ stopping on the point $$$A$$$ since the angle between the side $$$AB$$$ and the ground is $$$\epsilon = 153.43^{\circ} \geq 90^{\circ}$$$. Thus, he traveled $$$|CA| = \sqrt{5}$$$ on total.