409395: GYM103496 H Halcon Collider

H. Halcon Collidertime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

Try to guess the problem from the following gif: https://imgur.com/xtk06Dt

The Physics Departments in the Philippines' top universities decided that it was high time that the Philippines catch up with other countries' research facilities, so that Filipino physicists could also be at the frontier of new theoretical discoveries. Thus, they have teamed up to create the Great Halcon Collider, a particle accelerator constructed beneath the mountains of the Mindoro provinces.

Alice was fortunate enough to have been selected by her school to be a student delegate who will be one of the first to tour the brand new facilities. However, the head scientists at the Great Halcon Collider were concerned about letting untrained teenagers onto their multi-billion peso facilities. Thus, they decided to administer the following test, and would only allow entry to the students who answer it correctly.

A positron particle, modeled as a point, begins in the bottom-left corner of a box with horizontal width $$$w$$$ and vertical height $$$h$$$. The particle moves continuously in a straight line at a constant velocity. Initially, the particle has a horizontal velocity of $$$x$$$ units per second, and a vertical velocity of $$$y$$$ units per second, where $$$x$$$ and $$$y$$$ are positive integers.

When the positron hits an edge of the box, it bounces off such that the angle of incidence is equal to the angle of reflection (see diagram). When it hits a corner of the box, it vanishes. The scientists request the following information from Alice.

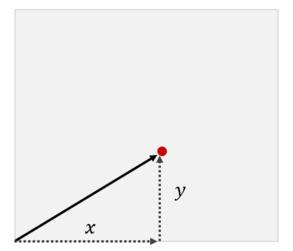
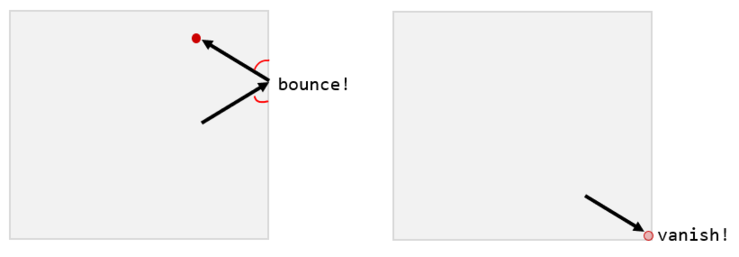
• What is the total distance traveled by the positron before vanishing?
• How many times did the positron bounce off a side of the box?
• Which of the four corners did the positron vanish at?

Oh, also, maybe that's too easy. Alice will be asked to answer this question for $$$t$$$ different test cases.

Alice really wants to see the Great Halcon Collider, so she's asked for your help!

Input

Input begins with a single line, containing a single integer $$$t$$$.

Then, $$$t$$$ lines follow, each describing a test case. Each line contains the four space-separated integers $$$w$$$, $$$h$$$, $$$x$$$, $$$y$$$, respectively, for that test case.

Output

For each query, output three lines, answering each of the scientists' questions.

• First, output a real number, the total distance (in units) traveled by the positron before vanishing.
• Then, output an integer, the number of times the positron bounced off a side of the box.
• Finally, output a string denoting which corner the positron vanished at. This should be one of TL, TR, BL, BR, which correspond to the top-left, top-right, bottom-left, and bottom-right corner, respectively.

Your output will be considered correct if, for the answers to each test case, your distance has a relative error of at most $$$10^{-3}$$$, and the other two values are exactly correct. If your distance is $$$a$$$ and the judge's distance is $$$b$$$, then the relative error is $$$\dfrac{|a-b|}{b}$$$.Scoring

$$$$$$\begin{align*}

&\begin{array}{|l|} \hline \text{Constraints For All Subtasks} \\ \hline 1 \leq t \leq 1000 \\ \text{$1 \leq w, h, x, y \leq 1000$ for all test cases.} \\ \hline \end{array}\\

&\begin{array}{|c|c|l|} \hline \text{Subtask} & \text{Points} & \text{Constraints} \\ \hline 1 & \mathbf{30} & \text{$x = y = 1$ for all test cases.} \\ \hline 2 & \mathbf{30} & \text{$w = h = 1$ for all test cases.} \\ \hline 3 & \mathbf{30} & \text{$1 \leq w, h, x, y \leq 10$ for all test cases.} \\ \hline 4 & \mathbf{10} & \text{No further constraints.} \\ \hline \end{array}\\

\end{align*}$$$$$$

ExamplesInput

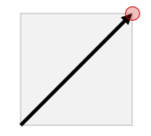
1
1 1 1 1

Output

1.414213562373
0
TR

Input

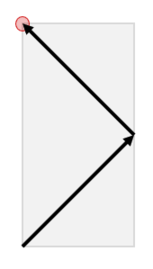
3
1 2 1 1
1 3 2 4
4 3 5 2

Output

2.828427124746
1
TL
6.708203932499
3
BR
64.621977685614
21
BR

Note

The positron travels as follows in the first sample input.

The positron travels as follows in the first test case of the second sample input.

The positron travels as follows in the second test case of the second sample input.

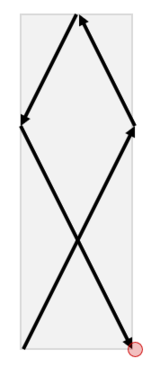
An animated gif of the positron's trajectory in the third test case of the second sample input has been uploaded here: https://imgur.com/xtk06Dt. This is the same gif shown at the beginning of the problem statement.