409400: GYM103496 M Mondrianansala
Description
Bob's art teacher tasked him with creating a collection of artworks that imitate the style of Vicente Manansala, one of the Philippines' national artists. As Manansala was a cubist, Bob worked hard to create a style that uses sharp geometric shapes to present a stylized and deconstructed perspective of the world.
Unfortunately, Bob is a better programmer than he is an artist. He leaned too hard into the "geometric shapes" idea, and the artworks he created were composed of only rectangles. His art teacher commented that Bob's paintings more closely resembled the abstract works of Piet Mondrian instead. Undeterred, Bob decided to call his new style Mondrianansala.
A rectangle is of the Mondrianansala style if it has integer unit dimensions, and the ratio of its shorter side to its longer side is exactly $$$2 : 3$$$ (so it could be $$$2 \times 3$$$ or $$$6 \times 4$$$, or $$$6 \times 9$$$, or $$$300 \times 200$$$, etc.). We say that an entire painting is of the Mondrianansala style if it satisfies the following conditions.
- It is painted on a square canvas.
- The painting is entirely composed of Mondrianansala-style rectangles.
- Each rectangle is one of $$$26$$$ different colors, and the entire rectangle is painted that color.
- No two touching rectangles have the same color (though rectangles of the same color may touch at corners).
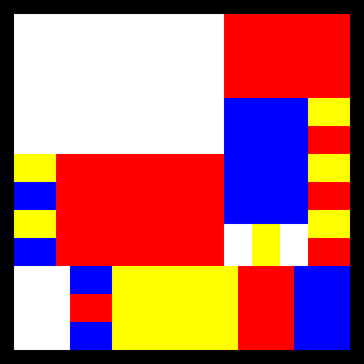
Bob's running out of time, and he needs a lot of different Mondrianansala-style paintings for his exhibit. Can you write a program that, given a positive integer $$$m$$$, creates a Mondrianansala-style painting with exactly $$$m$$$ rectangles? You can even choose the size of the painting (within reason). Bob managed to prove that the task should always be possible when $$$m \geq 6$$$.
InputInput consists of a single line containing the integer $$$m$$$.
OutputOutput the painting. We will treat the painting as a pixelmap and represent it as an ASCII grid.
Output a line containing a single integer $$$n$$$, the side lengths of the painting. Then, output $$$n$$$ lines, each containing a string with $$$n$$$ uppercase English letters, representing the painting. Two pixels are considered the same color if they are represented by the same letter. Contiguous regions of pixels of the same color correspond to the rectangles.
We can show that, given the constraints, a solution always exists that satisfies $$$1 \leq n \leq 2500$$$. If there are multiple solutions, output any of them that have $$$n$$$ in this range.
Note: Because of the possibly huge output, it is recommended that Python users submit to PyPy.
Scoring$$$$$$\begin{align*}
&\begin{array}{|c|c|l|} \hline \text{Subtask} & \text{Points} & \text{Constraints} \\ \hline 1 & \mathbf{25} & m=6\text{ or }m=12 \\ \hline 2 & \mathbf{20} & m=6\text{ or }m=2022 \\ \hline 3 & \mathbf{15} & m=6\text{ or }m=2038 \\ \hline 4 & \mathbf{15} & m=6\text{ or }m=5000 \\ \hline 5 & \mathbf{10} & 6 \leq m \leq 5000 \\ \hline 6 & \mathbf{15} & 6 \leq m \leq 2\times 10^5 \\ \hline \end{array}\\
\end{align*}$$$$$$
6Output
6 AAABBB AAABBB BBBAAA BBBAAA AAABBB AAABBBInput
24Output
24 AAAAAAAAAAAAAAABBBBBBBBB AAAAAAAAAAAAAAABBBBBBBBB AAAAAAAAAAAAAAABBBBBBBBB AAAAAAAAAAAAAAABBBBBBBBB AAAAAAAAAAAAAAABBBBBBBBB AAAAAAAAAAAAAAABBBBBBBBB AAAAAAAAAAAAAAACCCCCCDDD AAAAAAAAAAAAAAACCCCCCDDD AAAAAAAAAAAAAAACCCCCCBBB AAAAAAAAAAAAAAACCCCCCBBB DDDBBBBBBBBBBBBCCCCCCDDD DDDBBBBBBBBBBBBCCCCCCDDD CCCBBBBBBBBBBBBCCCCCCBBB CCCBBBBBBBBBBBBCCCCCCBBB DDDBBBBBBBBBBBBCCCCCCDDD DDDBBBBBBBBBBBBAADDAADDD CCCBBBBBBBBBBBBAADDAABBB CCCBBBBBBBBBBBBAADDAABBB AAAACCCDDDDDDDDDBBBBCCCC AAAACCCDDDDDDDDDBBBBCCCC AAAABBBDDDDDDDDDBBBBCCCC AAAABBBDDDDDDDDDBBBBCCCC AAAACCCDDDDDDDDDBBBBCCCC AAAACCCDDDDDDDDDBBBBCCCCNote
The second sample output corresponds to the $$$m = 24$$$ image shown in the problem statement.