409476: GYM103577 B Blockchain

Proof-of-work (PoW in short) systems are used in blockchains to add valid blocks into a distributed ledger (the block chain). A block is assumed to be valid if a miner (the first, out of multiple miners) solves a difficult cryptographic puzzle, hence "proving" they have done a significant amount of computation (proof of work) before a new block is added.

Elon had a dream about a new cryptographic puzzle the other day and has decided to set up a new blockchain system for a new social network, Dogebook. On Dogebook, each block added to the blockchain consists of an undirected graph representing users, and edges representing how much they like each other (possibly multiple edges between the same pair of nodes). The puzzle Elon dreamt of is as follows: given a graph $$$G$$$ composed of edges $$$E$$$ and a function $$$w(e)$$$ which represents the weight of an edge $$$e \in E$$$ , calculate the following function:

$$$$$$H(E, w) = \max_{E' \subseteq E} \prod_{e \in E'} w(e) \times p(w(e))$$$$$$ where $$$p(x) = 1$$$ if $$$x=2k+1$$$ for some non negative integer $$$k$$$, otherwise $$$p(x) = 0$$$.

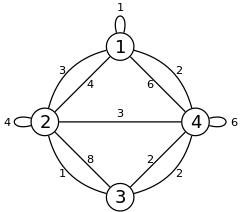$$$H(E, w) = = (3 \times 1) \times (3 \times 1) \times (1 \times 1)= 9$$$

In the example above, one possible $$$E'$$$ that maximizes $$$\prod_{e \in E'} w(e) \times p(w(e))$$$ consist of the subset with the edge of weight $$$3$$$ between $$$1$$$ and $$$2$$$, the edge of weight $$$3$$$ between $$$2$$$ and $$$4$$$ and the edge of weight $$$1$$$ between $$$1$$$ and $$$1$$$.

Elon is convinced this system is foolproof and will make a lot of money. Tomi, a very resourceful dog-hacker, disagrees and thinks it is a waste of time. Tomi is convinced he can hack this system by solving the puzzle very fast, rendering the PoW meaningless. However, Tomi is busy running around with Eli and Rafa (see problem H), can you help Tomi to break the puzzle?

The input will contain several graphs. Each graphs begins with $$$n$$$ and $$$m$$$ ($$$1 \leq n, m \leq 10^5$$$) separated by a whitespace, representing the number of nodes and the number of edges, respectively. Next, there will be $$$m$$$ lines with three integers $$$w$$$, $$$u$$$ and $$$v$$$ ($$$1 \leq u, v \leq 10^5$$$, $$$1 \leq w \leq 10^9$$$), representing an edge between $$$u$$$ and $$$v$$$ with weight $$$w$$$.

For each graph, you must print a line with a single integer, the value of $$$H(G, w)$$$. It is guaranteed that each answer fits on a 32-bit signed integer. Print an end of line character after each answer.

4 12
1 1 1
4 2 2
6 4 4
4 2 1
6 1 4
8 2 3
2 4 3
3 2 4
3 1 2
2 1 4
2 3 4
1 2 3

9