409585: GYM103640 A Ancient Towers

The king of Nlogonia has conquered many lands throughout his life, and now that his son has come of age, the king wants to share his possessions with him.

Nlogonia has $$$N$$$ ancient towers that can be seen as points in the Cartesian plane. The king decided that his son must choose four of those towers. Then the son must build a wall connecting the towers, so as to form a (simple but not necessarily convex) quadrilateral with the towers as vertices. The land surrounded by the wall will be owned by the son. Since the king does not want people making fun of his son for not having enough land, the area of the quadrilateral must be greater than or equal to a given value $$$S$$$.

The son is eager to choose his portion of the land, but the king wants to know beforehand in how many different ways this can be done. The picture below shows an example with $$$N=4$$$ towers. In this case, there are two different quadrilaterals with an area of at least $$$S=2$$$.

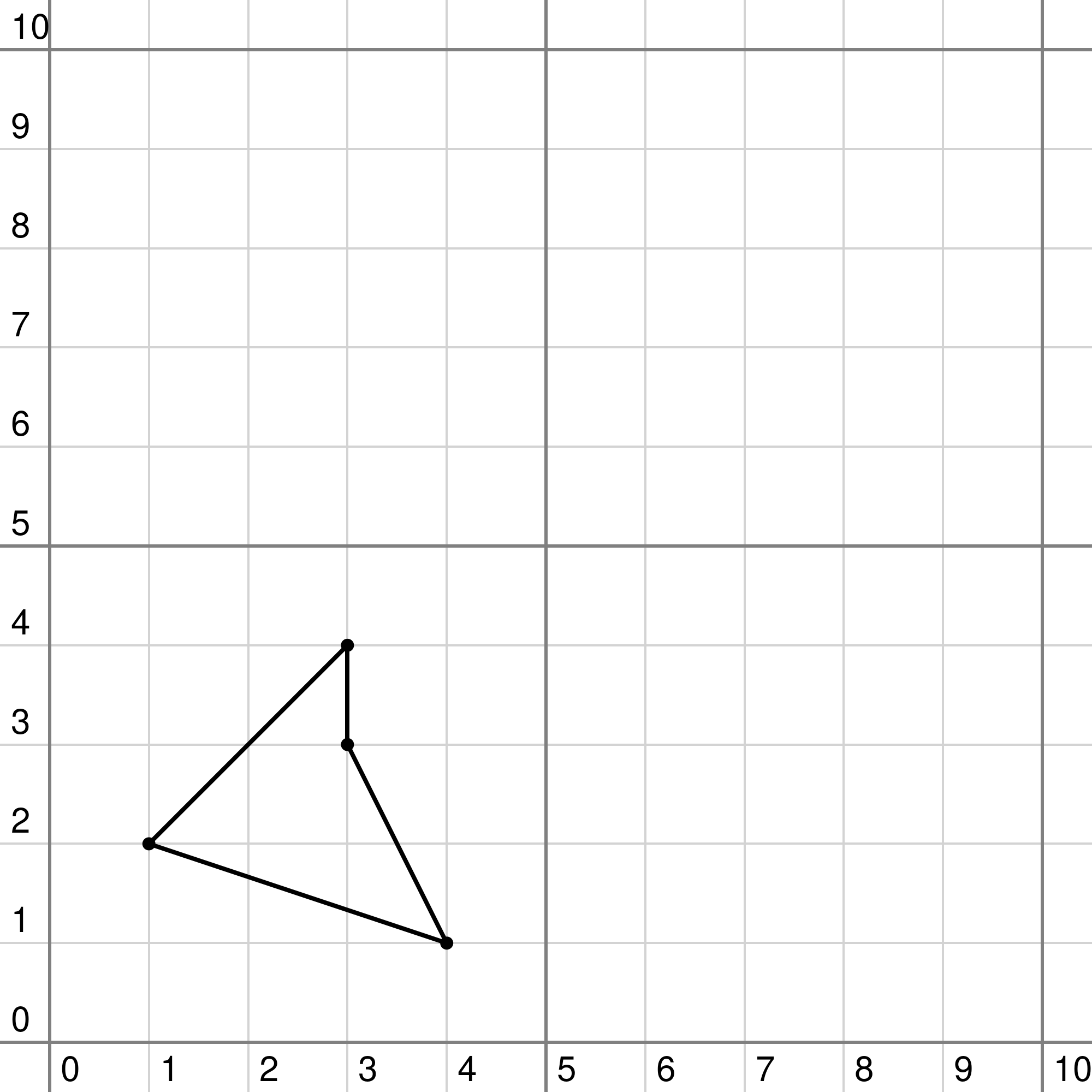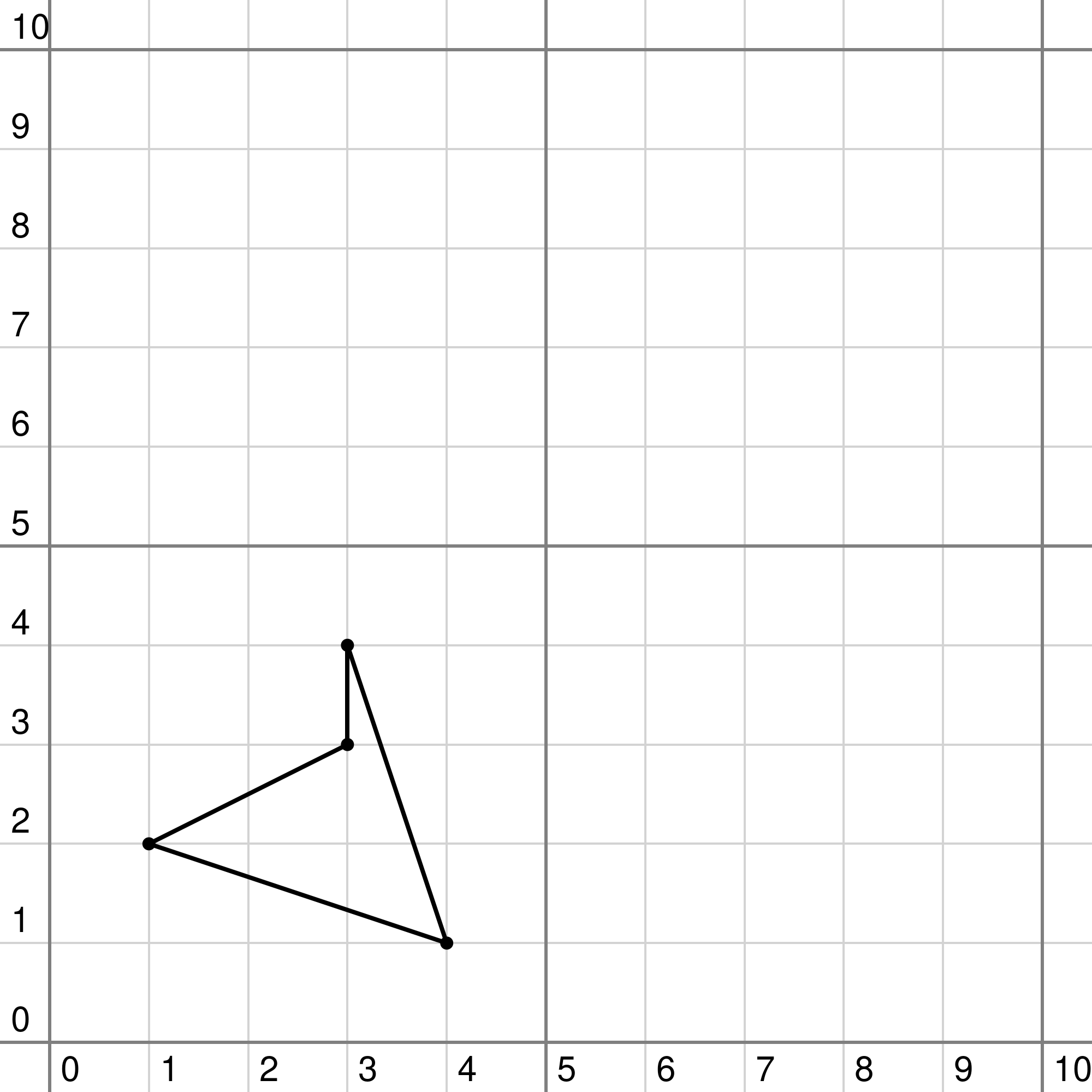The first line contains two integers $$$S$$$ ($$$1 \leq S \leq 10^{18}$$$) and $$$N$$$ ($$$4 \leq N \leq 400$$$), indicating respectively the minimum area and the number of ancient towers. Each of the next $$$N$$$ lines describes a tower with two integers $$$X$$$ and $$$Y$$$ ($$$0 \leq X, Y \leq 10^9$$$), denoting the coordinates of the tower. No two towers have the same location, and no three of them are collinear.

Output a single line with an integer indicating the number of different simple quadrilaterals having towers as vertices and area at least $$$S$$$. A quadrilateral is simple if non-contiguous edges do not intersect. Two quadrilaterals are considered different if they have different vertices or different edges.

2 4
1 2
3 4
3 3
4 1

2

1 4
1 2
3 4
3 3
4 1

3

4 5
1 1
3 3
3 0
0 1
1 0

3

1 4
0 0
1000 0
0 1000
1000 1000

1