409654: GYM103660 G Guaba and Computational Geometry

There are $$$n$$$ rectangles on a two-dimensional plane. The $$$i$$$-th rectangle has a weight $$$w_i$$$. You should find $$$2$$$ non-overlapping rectangles $$$i$$$ and $$$j$$$, and make $$$w_i+w_j$$$ as large as possible.

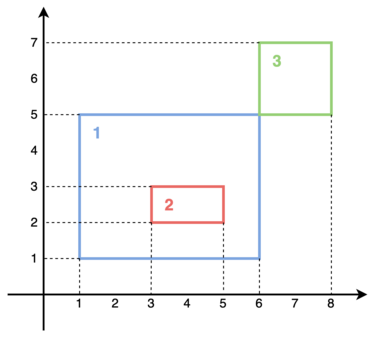
$$$2$$$ rectangles are non-overlapping if and only if no points are inside both rectangles at the same time. For example, rectangles $$$1$$$ and $$$3$$$ are overlapping, as are rectangles $$$1$$$ and $$$2$$$, but rectangles $$$2$$$ and $$$3$$$ are not overlapping.

The first line contains an integer $$$T(1\le T\le 3\times 10^5)$$$ — the number of test cases.

For each test case, the first line contains an integer $$$n(1\le n\le 3\times 10^5)$$$ — the number of rectangles.

Then $$$n$$$ lines follow, each line contains $$$4$$$ integers $$$a_i,b_i,c_i,d_i(-10^9\leq a_i, b_i, c_i, d_i\le 10^9, a_i<c_i, b_i<d_i)$$$ — the lower left corner $$$(a_i,b_i)$$$ and upper right corner $$$(c_i,d_i)$$$.

The next line contains $$$n$$$ integers $$$w_i(1\le w_i\le 10^9)$$$ — the weight of the $$$i$$$-th rectangle.

It is guaranteed that $$$\sum n\leq 3\times 10^5$$$ over all test cases.

For each test case, output an integer in one line — the maximum value of $$$w_i+w_j$$$. If all rectangles overlap each other, output $$$-1$$$.

3
3
1 1 6 5
3 2 5 3
6 5 8 7
10 1 2
2
1 1 6 5
6 5 8 7
1 2
1
-1 -1 1 1
1000000000

3
-1
-1