409702: GYM103688 D Collision Detector
Description
Joseph loves physics. And one day, while Joseph was playing ping-pong, he was obsessed with the study of the collision of two balls.
He found the collision of any two of the balls is completely elastic, which means there is no kinetic energy loss and the sum of the momentum remains the same after the collision.
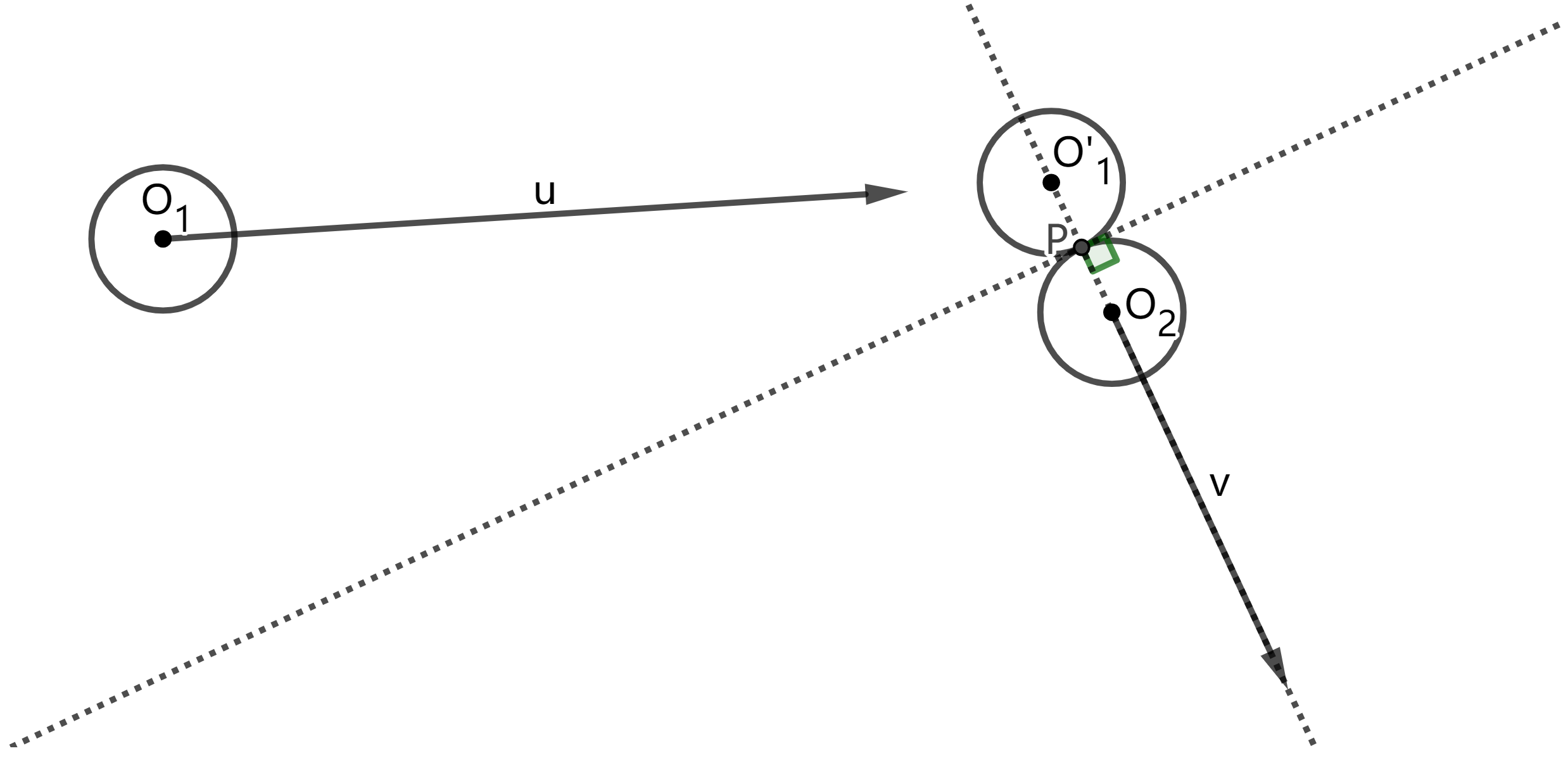
However, you only need to consider a simpler case in this problem. If we regard all ping-pong balls as the circles of radius $$$1$$$ on the two-dimensional plane, the collision of a moving ball and a static ball can be described by the figure below. Ball $$$O_1$$$ has the speed $$$\boldsymbol{u}$$$ initially, and then it hits a static ball $$$O_2$$$ at the point $$$P$$$. Let the tangent(切线) of circle $$$O_2$$$ at point $$$P$$$ be $$$l$$$. The speed of ball $$$O_2$$$ after collision will be a speed of $$$\boldsymbol{v}$$$ which is perpendicular(垂直) to $$$l$$$.
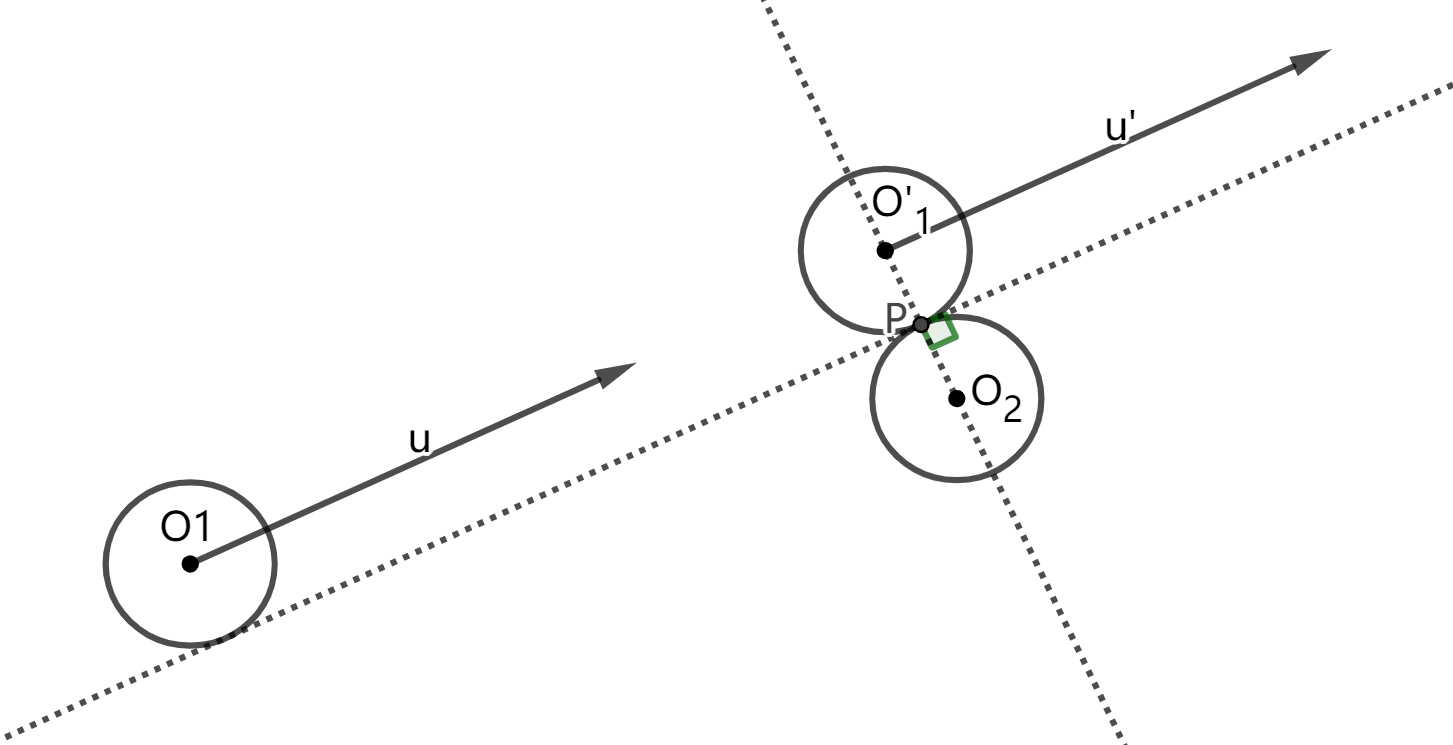
Particularly, if the trail of $$$O_1$$$ is just tangent to $$$O_2$$$ (see the figure below), there will be no collision.
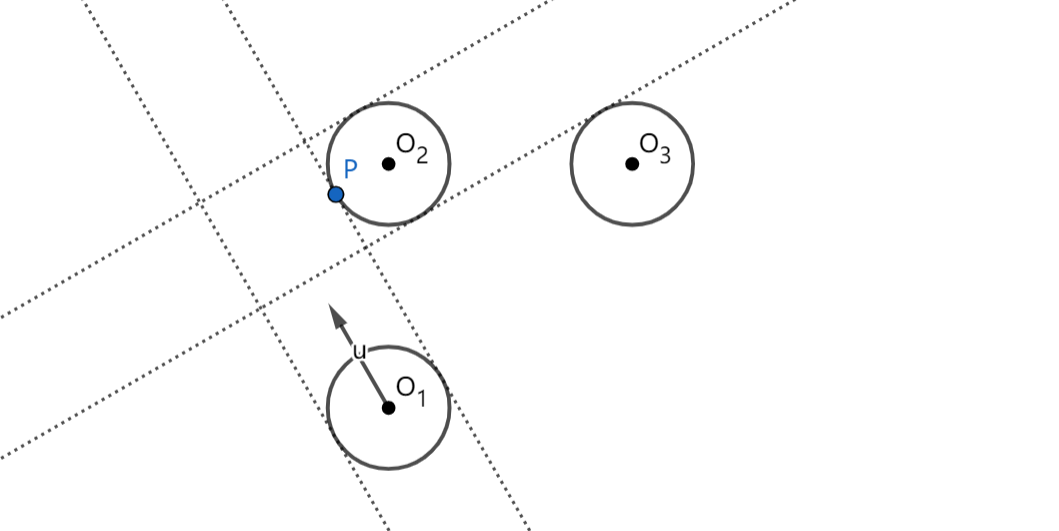
Now Joseph put three static balls $$$O_1, O_2, O_3$$$ on the table. He wants to give the ball $$$O_1$$$ an initial speed $$$u$$$ and see if it can hit $$$O_2$$$ and let $$$O_2$$$ finally hit $$$O_3$$$. Please write a program to tell him whether the initial speed exists.
InputThe first line of the input gives the number of test cases, $$$T ~ (1 \leq T \leq 10^3)$$$. $$$T$$$ test cases follow.
For each test case, only one line contains six integers $$$x_1, y_1, x_2, y_2, x_3, y_3$$$, which indicates the coordinate of $$$O_1, O_2, O_3$$$ are $$$(x_1, y_1), (x_2, y_2), (x_3, y_3)$$$ respectively. It's guaranteed that the input circles do not intersect.
All of the $$$x_i$$$ and $$$y_i$$$ are in the range $$$[0, 10^4]$$$.
OutputPrint yes if there exists an initial speed of $$$O_1$$$ such that $$$O_1$$$ can hit $$$O_2$$$, and then $$$O_2$$$ moves to hit $$$O_3$$$ finally, otherwise print no.
ExampleInput4 7 2 4 2 1 2 2 8 3 5 3 0 1 1 1 5 5 5 0 0 2 2 6 0Output
yes yes no noNote
For the first testcase, one possible initial speed of $$$O_1$$$ can be $$$(-1,0)$$$.
For the second testcase, one possible initial speed of $$$O_1$$$ can be $$$(1, -1)$$$
The figure below shows the third testcase. In the only solution the trail of $$$O_1$$$ is tangent to $$$O_2$$$, so the collision cannot happen,