409775: GYM103741 E Ellipse

There are $$$n$$$ points $$$P_0,P_1,\dots,P_{n-1}$$$ on a plane, and the coordinates of $$$P_{i}$$$ are $$$(x_i,y_i)\ (0\le i<n)$$$.

Let $$$M=(\sum_{0\le i<n} x_i, \sum_{0\le i<n} y_i)/n$$$, i.e., the mass center of the initial $$$n$$$ points. The following operations will repeat for $$$k$$$ times:

• For each $$$0\le i<n$$$, extend segment $$$MP_i$$$ to $$$Q_i$$$ such that $$$|MP_i|=\cos(2\pi/n)\cdot |MQ_i|$$$.
• Let $$$Q_{-1}=Q_{n-1}$$$ and $$$Q_n=Q_0$$$. For each $$$0\le i<n$$$, replace $$$P_i$$$ with $$$R_i$$$, the mass center of $$$\triangle P_iQ_{i-1}Q_{i+1}$$$.

You can see the picture below for better understanding.

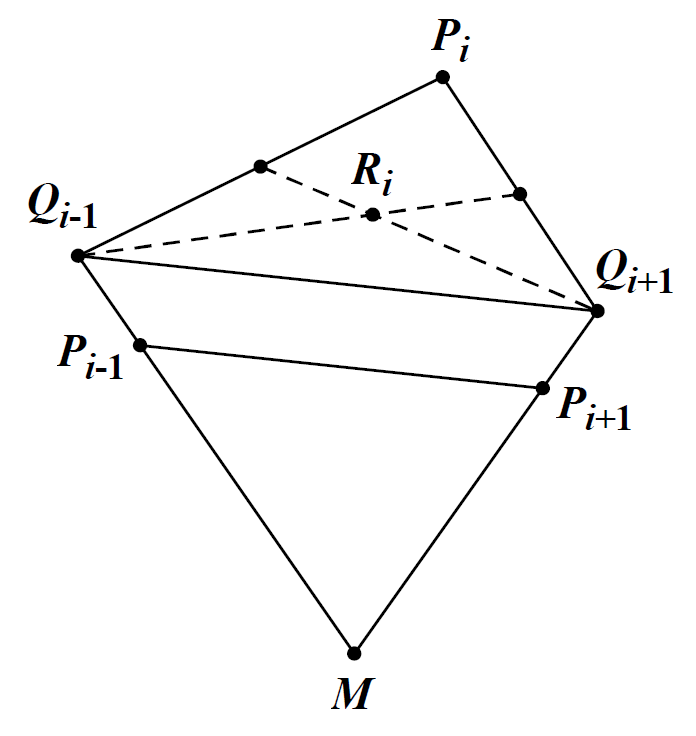Constructing $$$R_i$$$ from $$$P_{i-1}$$$, $$$P_i$$$ and $$$P_{i+1}$$$

Let $$$P'_i=\lim_{k\to\infty} P_i\ (0\le i<n)$$$ and $$$P'_n=P'_0$$$. It can be proved that $$$P'_i$$$ will always exist when $$$n\ge 7$$$. Now you need to output the value of

$$$$$$ \sum_{0\le i<n} \mathop{MP'_i}^{-\hspace{-2pt}-\hspace{-2pt}-\hspace{-2pt}\rightarrow} \times \mathop{MP'_{i+1}}^{-\hspace{-2pt}-\hspace{-2pt}-\hspace{-2pt}\rightarrow\ \ \ } $$$$$$

P.S. You can try to prove that all $$$P'_i$$$ will be on a certain ellipse though it may have nothing to do with the problem.

The first line contains an integer $$$n\ (7\le n\le 10^6)$$$, the number of points.

The $$$i$$$-th of the next $$$n$$$ lines contains two integers $$$x_i$$$ and $$$y_i\ (|x_i|,|y_i|\le 10^5)$$$, the initial coordinates of $$$P_i$$$.

Output a real number as the answer. Your answer will be considered correct if and only if the absolute or relative error of your answer to the correct answer is less than or equal to $$$10^{-6}$$$.

8
1 -1
0 -2
-1 -1
-2 0
-1 1
0 2
1 1
2 0

-16.485281374

7
2 0
-2 1
2 -2
0 4
-3 -2
-2 -3
3 1

8.192914574

In the first example, the $$$8$$$ points will be on a circle of radius $$$1.70709$$$ centered at $$$(0,0)$$$ after infinite operations.