409895: GYM103828 H Kite
Description
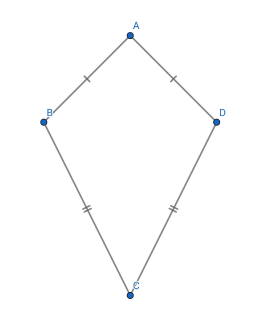 The picture is to show the shape of the kite.
The picture is to show the shape of the kite. Given an integer $$$n$$$, count the number of different kites in a regular $$$n$$$-gon.
A regular $$$n$$$-gon is a convex polygon consisting of $$$n$$$ equal-length sides and all its angles are equal.
A kite is a convex quadrilateral $$$A$$$ $$$B$$$ $$$C$$$ $$$D$$$, such that $$$AB = AD$$$ and $$$CB = CD$$$.
Two kites are considered different if they differ by at least one point.
InputThe first line of the input contains a single integer $$$T \space (1 \le T \le 2 \cdot 10^5)$$$ - the number of test cases.
Then $$$T$$$ lines follow, each containing a single integer $$$n \space (4 \le n \le 10^9)$$$ - the number of sides of the polygon.
OutputFor each test case, print a single line containing the number of different kites in a regular $$$n$$$-gon.
ExampleInput2 4 5Output
1 0Note
Explanation of the sample:
In the first testcase, the only kite is the whole $$$4$$$-gon.
In the second testcase, there are no kites.