409968: GYM103870 M Driving
Description
In his quest to become the better TA, Thomas suddenly received inspiration: "What if he tried to learn from someone who was already a teacher?". Thomas immediately thought of teacher and realized if he wanted to become a better TA, he had to be driving at all times. (Note that Thomas has tried biking as a greener method of transport, but that failed).
Thomas currently lives in a country with $$$N$$$ cities and $$$M$$$ roads between cities. Every road also has a parameter $$$t$$$, denoting the number of minutes to pass through a road.
Consider a road trip from some city $$$u$$$ to city $$$v$$$. Let us assume that Thomas has unlimited mileage from infinite money and the only thing limiting his drives is his patience. If Thomas's patience is $$$p$$$, he can only drive on roads that require $$$p$$$ minutes to drive through. For instance having patience $$$3$$$ can enable Thomas to travel through roads that take $$$1$$$, $$$2$$$, or $$$3$$$ minutes to cross.
Now Thomas has a list of cool cities that is initially empty but is always growing. He will make $$$Q$$$ additions to that list. After each addition, he asks what the minimum patience he needs to make a road trip between any two cool cities is. Note that Thomas is picking two cities and then traveling between them, not taking the answer over all pairs of cities.
InputThe first line contains three integers $$$N$$$, $$$M$$$, $$$Q$$$ $$$(1 \leq Q \leq N \leq 10^5, 1 \leq M \leq 2 \cdot 10^5)$$$ denoting the number of cities, roads, and additions to the list respectively.
The following $$$M$$$ lines contain three integers each, $$$u$$$, $$$v$$$, $$$t$$$ $$$(1 \leq u \neq v \leq N, 1 \leq t \leq 10^9)$$$ the two cities this road connects as well as the number of minutes needed to traverse it. Note that the graph may have multiedges.
The following $$$Q$$$ lines each contain one integer, $$$x$$$ $$$(1 \leq x \leq N)$$$, the new city Thomas considers cool. It is guaranteed Thomas never adds the same city twice to his list.
For tests $$$1 - 3$$$, $$$(1 \leq Q \leq 10)$$$.
For tests $$$4 - 7$$$, $$$(1 \leq t \leq 2)$$$.
For tests $$$8 - 10$$$, $$$|u - v| = 1$$$ for all edges.
The remaining test cases do not satisfy any additional constraints.
OutputOutput $$$Q$$$ lines, each line containing one integer, denoting the minimum amount of patience needed to make a road trip between any two cool cities. Output $$$-1$$$ if it is impossible to make such a trip.
ExampleInput5 7 3 1 2 3 2 4 2 3 5 4 1 5 10 3 4 7 4 5 6 2 5 6 4 3 1Output
-1 6 3Note
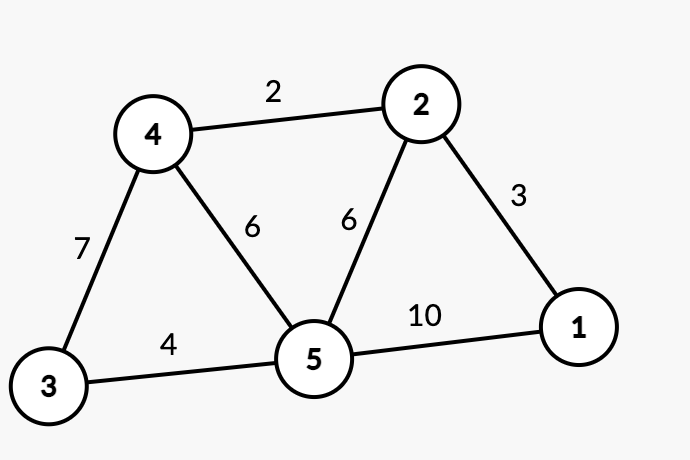
After adding the first cool city, $$$4$$$, there is only 1 city so Thomas cannot make any trip.
After adding the second cool city, $$$3$$$, Thomas can make the trip $$$4 \rightarrow 5$$$, $$$5 \rightarrow 3$$$ only using patience $$$6$$$. Note that going from $$$4 \rightarrow 3$$$ would take patience $$$7$$$. Thomas can also reach cities $$$2$$$ and $$$3$$$ with $$$6$$$ patience, although there isn't much of a point in going there.
After adding the third cool city, $$$1$$$, Thomas can make the trip $$$4 \rightarrow 2$$$, $$$2 \rightarrow 1$$$ with patience $$$3$$$.
—
Idea: 3366
Preparation: 3366
Occurrences: Advanced 6