409990: GYM103886 Q Cereal Trees II

Envy has found an apple tree, but unfortunately, finds out that the apples are not ripe at all. Because he has a huge sweet tooth, and is craving something sugary, he decides to turn the apples into cereal!

Although he does not know how to do this, he consults the all-knowing Larry. Larry confides in Envy that he will give him the ancient Apple Method needed to make cereal, if Envy solves the following question:

You are given a tree of $$$n$$$ ($$$1 \leq {n} \leq {5 \cdot 10^3}$$$) nodes, numbered $$$1 \dots n$$$, and $$$n-1$$$ edges.

You want to visit every node in this tree exactly once. You can start at any node, and jump from any node to any other node.

A jump is considered magical if the node that you move to is within the subtree of the node you are currently on.

You are given $$$q$$$ queries, where the $$$i$$$th query gives you two numbers $$$x_i$$$ and $$$y_i$$$.

For each query, compute the number of paths visiting every nodes in the subtree of node $$$x$$$ (including $$$x$$$) with exactly $$$y$$$ magical jumps.

Note that ($$$1 \leq x \leq n$$$) and $$$y$$$ is strictly less than the number of nodes in the subtree of $$$x$$$ ($$$y$$$ can be $$$0$$$).

Since this number can be quite large, find it modulo $$$10^9 + 7$$$.

The first line contain $$$n$$$.

The next $$$n - 1$$$ lines contains two integers $$$a$$$ and $$$b$$$, meaning that the $$$a$$$th node is connected to the $$$b$$$th node.

The next line will contain an integer $$$q (1 \leq q \leq 5000)$$$.

The next $$$q$$$ lines will contain two integers $$$x_i$$$ and $$$y_i$$$.

Note: the tree is rooted at node $$$1$$$.

For every query of the form $$$x_i$$$, $$$y_i$$$, compute the number of paths visiting every node in the subtree of $$$x$$$ exactly once such that the path contains $$$y$$$ magical jumps, modulo $$$10^9 + 7$$$.

Each answer for a distinct query should be on a newline.

4
1 2
2 3
2 4
3
2 0
2 1
2 2

2
4
0

The graph below represents the tree described in the sample input.

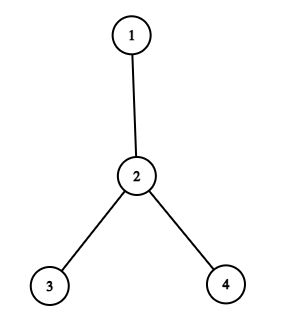
For the first query, the two possible paths are $$$4 \rightarrow 3 \rightarrow 2$$$ and $$$3 \rightarrow 4 \rightarrow 2$$$.

Problem Credits: Larry Xing