410204: GYM103973 N Coloring
Description
Walk Alone is poor at graph theory. In today's graph theory class, Walk Alone is given a graph with $$$n$$$ vertices and $$$m$$$ edges, and he is required to color all vertices red or blue so that each edge has endpoints of differing colors. It is guaranteed that such coloring strategy always exists, i.e., the graph is bipartite. It is a simple task indeed, but Walk Alone colored some vertices incorrectly, so he is asking you for help.
In his bipartite graph, some vertices are colored red, some are colored blue, and the others are not colored yet. Since a colored vertex cannot change its color, your task is to remove as few vertices as possible (as well as the edges connecting with them), so that it is possible to color all uncolored vertices, and each edge should have endpoints of differing colors after that.
InputThe first line contains two integers $$$n\ (1\le n\le 10^4)$$$ and $$$m\ (1\le m\le 10^4)$$$, the number of vertices and edges in the original graph.
The second line contains $$$n$$$ integers. The $$$i$$$-th integer $$$c_i$$$ indecates the color of the $$$i$$$-th vertex: $$$1$$$ for red, $$$2$$$ for blue, and $$$0$$$ if the vertex is not colored.
Each of the next $$$m$$$ lines contains two integers $$$u$$$ and $$$v\ (1\le u,v\le n)$$$, indicating an edge between vertex $$$u$$$ and $$$v$$$. It is guaranteed that the given graph is bipartite.
OutputPrint the minimum number of vertices you need to remove in the first line, and the label of removed vertices separated by spaces in the second line. If there exists multiple solutions, output any of them.
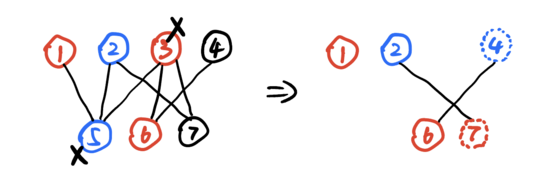
ExamplesInput7 7 1 2 1 0 2 1 0 1 5 2 5 3 5 3 6 4 6 2 7 3 7Output
2 3 5Input
5 4 1 1 2 2 0 5 1 5 2 5 3 5 4Output
1 5Input
3 2 0 0 1 1 2 2 3Output
0Note
Here is an illustration for the first example: