410302: GYM104003 J William and Rangoli

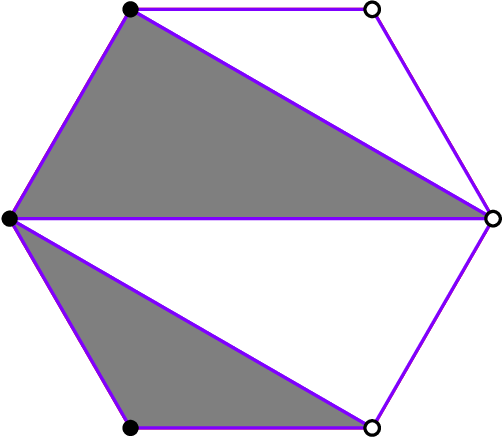
For celebrating Diwali, William created rangoli in the shape of a regular polygon with $$$n$$$ vertices, where $$$n$$$ is even. $$$m$$$ of the vertices of the polygon in a row are all white, and the remaining $$$n - m$$$ nodes are black. Each of the edges of the polygon are connected with purple lines.

To fill in the polygon, William first creates a triangulation of the polygon, again using purple edges and only drawing non-intersecting diagonals. Now, William fills in the each of the triangles. If all three vertices of the triangle are the same color, William is unhappy, so the triangulation would be invalid. Otherwise, if there are 2 black vertices and 1 white vertex, the triangle is colored black. Similarly, if there are 2 white vertices and 1 black vertex, the triangle is colored white. In the end, William wants there to be $$$k$$$ white triangles and $$$n - k - 2$$$ black triangles for the triangulation to be valid.

William is having trouble deciding which triangulation he wants to use. How many possible valid triangulations are there? Because the answer may be large, compute it modulo $$$10^9 + 7$$$.

The first and only line contains three integers $$$n$$$, $$$m$$$, and $$$k$$$ ($$$3 \leq n \leq 2 \cdot 10^5$$$, $$$0 \leq m \leq n$$$, $$$0 \leq k \leq n - 2$$$) — the number of vertices in the polygon, the number of white vertices, and the required number of white triangles.

Output a single integer — the total number of valid triangulations, modulo $$$10^9 + 7$$$.

6 3 2

6

Below is an image of a valid triangulation for the sample test case: