410532: GYM104036 2 Раскрашенный куб
Description
Поверхность куба со стороной $$$n$$$ см покрасили снаружи в синий цвет (со всех шести сторон). После этого его распилили на кубики со стороной 1 см. В результате получились части, у которых синим цветом окрашены 0, 1, 2 или 3 стороны. Посчитайте количество кубиков указанного вида.
Входные данныеПервая строка содержит натуральное число $$$n$$$ ($$$2 \le n \le 1000$$$) – размер кубика.
Вторая строка содержит неотрицательное целое число $$$f$$$ ($$$0 \le f \le 3$$$) – количество окрашенных граней у кубиков, число которых нужно посчитать.
Выходные данныеВыведите одно неотрицательное целое число – ответ на вопрос задачи. Гарантируется, что оно не превосходит $$$10^9$$$.
Система оценкиРешения, правильно работающие, когда число $$$f$$$ равно 0, будут оцениваться в 30 баллов.
Решения, правильно работающие, когда число $$$f$$$ равно 1, будут оцениваться в 30 баллов.
Решения, правильно работающие, когда число $$$f$$$ равно 2, будут оцениваться в 30 баллов.
Решения, правильно работающие, когда число $$$f$$$ равно 3, будут оцениваться в 10 баллов.
ПримерВходные данные3 1Выходные данные
6Примечание
В примере дано $$$n = 3$$$ и $$$f = 1$$$. Рассмотрим рисунок: куб $$$3 \times 3 \times 3$$$ покрасили и распилили на $$$3^3 = 27$$$ маленьких кубиков. Требуется определить, сколько таких кубиков имеют единственную синюю грань.
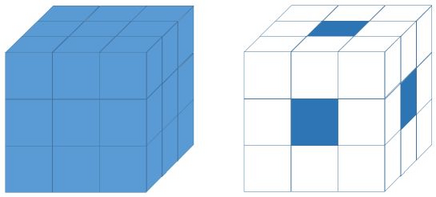
Это кубики, расположенные посередине каждой из шести граней, их ровно шесть.