410607: GYM104065 C Catch You Catch Me

Bobo accidentally dropped into the secret garden when he was listening to Song from a secret garden. Guess what did he see? Butterflies!

Yes, it is.

The structure of the secret garden can be modeled as an undirected tree of $$$n$$$ nodes labeled from $$$1$$$ to $$$n$$$, where the node labeled $$$1$$$ is the exit of the secret garden. There is initially a butterfly at each node labeled from $$$2$$$ to $$$n$$$. Bobo noticed that, at each minute, every butterfly would move through an edge towards the direction of the node labeled $$$1$$$. When a butterfly flies to the node labeled $$$1$$$, it leaves the secret garden and disappears forever.

Bobo wants to catch all the butterflies before they fly to the exit and disappear. Bobo is initially not at any node of the tree. What he can do is to choose any node of the tree at some minute (including minute $$$0$$$, where all butterflies are at their respective nodes) and catch all butterflies in that node (Bobo cannot catch butterflies at node $$$1$$$ as butterflies disappear instantly when they get there). This counts as an operation. Bobo acts really fast, and the time it takes for him to operate can be neglected. Bobo wonders, what is the minimum number of times he has to operate to catch all butterflies?

The first line contains an integer $$$n$$$ $$$(1\leq n\leq 10^5)$$$, denoting the number of nodes in the tree.

Then $$$n-1$$$ lines follow. Each line contains two integers $$$u,v$$$ $$$(1\leq u,v\leq n,u\neq v)$$$, denoting the number of edges in the tree.

It is guaranteed that the input forms a valid tree.

Output an integer in a line, denoting the minimum number of times Bobo has to operate to catch all butterflies.

5
1 2
2 3
2 4
1 5

3

For the first sample test case, the initial state at minute $$$0$$$ is shown as follows:

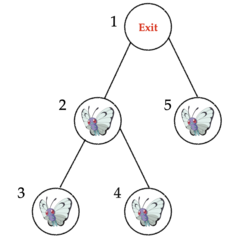
At minute $$$0$$$, Bobo must perform an operation on node $$$2$$$ and node $$$5$$$, otherwise the two butterflies at the two nodes will reach the exit in the next minute.

The two butterflies initially at nodes $$$3$$$ and $$$4$$$ both arrive at node $$$2$$$ at minute $$$1$$$. Then Bobo can perform one operation at node $$$2$$$ to catch them both. This takes three operations in all.