301834: CF346E. Doodle Jump
Memory Limit:256 MB
Time Limit:2 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Doodle Jump
题意翻译
有一个长度为 $n$ 的数列。 数列的第 $x$ 项为 $a\times x\bmod p$。 问将该数列排序后任意相邻两项之差的最大值是否 $\le h$。 多组询问,询问次数 $t$ 满足 $1\le t\le 10^4$。 $1\le a\le 10^9$,$1\le n<p\le 10^9$,$0\le h\le 10^9$。题目描述
In Doodle Jump the aim is to guide a four-legged creature called "The Doodler" up a never-ending series of platforms without falling. — Wikipedia. It is a very popular game and xiaodao likes it very much. One day when playing the game she wondered whether there exists a platform that the doodler couldn't reach due to the limits of its jumping ability. Consider the following problem. There are $ n $ platforms. The height of the $ x $ -th ( $ 1<=x<=n $ ) platform is $ a·x $ mod $ p $ , where $ a $ and $ p $ are positive co-prime integers. The maximum possible height of a Doodler's jump is $ h $ . That is, it can jump from height $ h_{1} $ to height $ h_{2} $ ( $ h_{1}<h_{2} $ ) if $ h_{2}-h_{1}<=h $ . Initially, the Doodler is on the ground, the height of which is 0. The question is whether it can reach the highest platform or not. For example, when $ a=7 $ , $ n=4 $ , $ p=12 $ , $ h=2 $ , the heights of the platforms are $ 7 $ , $ 2 $ , $ 9 $ , $ 4 $ as in the picture below. With the first jump the Doodler can jump to the platform at height $ 2 $ , with the second one the Doodler can jump to the platform at height $ 4 $ , but then it can't jump to any of the higher platforms. So, it can't reach the highest platform. 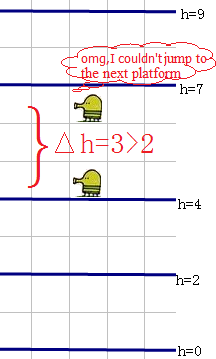User xiaodao thought about the problem for a long time but didn't solve it, so she asks you for help. Also, she has a lot of instances of the problem. Your task is solve all of these instances.输入输出格式
输入格式
The first line contains an integer $ t $ $ (1<=t<=10^{4}) $ — the number of problem instances. Each of the next $ t $ lines contains four integers $ a $ , $ n $ , $ p $ and $ h $ ( $ 1<=a<=10^{9} $ , $ 1<=n<p<=10^{9} $ , $ 0<=h<=10^{9} $ ). It's guaranteed that $ a $ and $ p $ are co-prime.
输出格式
For each problem instance, if the Doodler can reach the highest platform, output "YES", otherwise output "NO".
输入输出样例
输入样例 #1
3
7 4 12 2
7 1 9 4
7 4 12 3
输出样例 #1
NO
NO
YES