Doodle Jump

题意翻译

有一个长度为 $n$ 的数列。 数列的第 $x$ 项为 $a\times x\bmod p$。 问将该数列排序后任意相邻两项之差的最大值是否 $\le h$。 多组询问,询问次数 $t$ 满足 $1\le t\le 10^4$。 $1\le a\le 10^9$，$1\le n<p\le 10^9$，$0\le h\le 10^9$。

题目描述

In Doodle Jump the aim is to guide a four-legged creature called "The Doodler" up a never-ending series of platforms without falling. — Wikipedia. It is a very popular game and xiaodao likes it very much. One day when playing the game she wondered whether there exists a platform that the doodler couldn't reach due to the limits of its jumping ability. Consider the following problem. There are $ n $ platforms. The height of the $ x $ -th ( $ 1<=x<=n $ ) platform is $ a·x $ mod $ p $ , where $ a $ and $ p $ are positive co-prime integers. The maximum possible height of a Doodler's jump is $ h $ . That is, it can jump from height $ h_{1} $ to height $ h_{2} $ ( $ h_{1}&lt;h_{2} $ ) if $ h_{2}-h_{1}<=h $ . Initially, the Doodler is on the ground, the height of which is 0. The question is whether it can reach the highest platform or not. For example, when $ a=7 $ , $ n=4 $ , $ p=12 $ , $ h=2 $ , the heights of the platforms are $ 7 $ , $ 2 $ , $ 9 $ , $ 4 $ as in the picture below. With the first jump the Doodler can jump to the platform at height $ 2 $ , with the second one the Doodler can jump to the platform at height $ 4 $ , but then it can't jump to any of the higher platforms. So, it can't reach the highest platform. 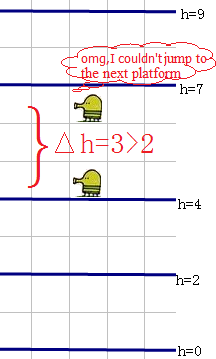User xiaodao thought about the problem for a long time but didn't solve it, so she asks you for help. Also, she has a lot of instances of the problem. Your task is solve all of these instances.

输入输出格式

输入格式

The first line contains an integer $ t $ $ (1<=t<=10^{4}) $ — the number of problem instances. Each of the next $ t $ lines contains four integers $ a $ , $ n $ , $ p $ and $ h $ ( $ 1<=a<=10^{9} $ , $ 1<=n&lt;p<=10^{9} $ , $ 0<=h<=10^{9} $ ). It's guaranteed that $ a $ and $ p $ are co-prime.

输出格式

For each problem instance, if the Doodler can reach the highest platform, output "YES", otherwise output "NO".

输入输出样例

输入样例 #1

3
7 4 12 2
7 1 9 4
7 4 12 3

输出样例 #1

NO
NO
YES

题意翻译

你在玩一个跳跃游戏，有 $n$ 块具有各自的高度的板子，第 $x$ 块板子的高度为 $(a\times x)\bmod p$。 你初始时在高度为 $0$ 的地面上，每次你可以跳到一个高度与你相差不超过 $h$ 的板子上。 你是否可以跳到最高的那块板子上？ 多组询问,询问次数 $t$ 满足 $1\le t\le 10^4$。 $1\le a\le 10^9$，$1\le n<p\le 10^9$，$0\le h\le 10^9$。