Rooks Defenders

题意翻译

你有个 $N \times N$ 的国际象棋棋盘。车可以防御所有同行同列的格子。 现在有 $Q$ 次操作或询问，每次给定一个 $T \in \{1, 2, 3\}$, 代表操作或询问类型： - 当 $T = 1$ 时，给定坐标 $(x, y)$, 表示在第 $x$ 行第 $y$ 列放置一枚车。 - 当 $T = 2$ 时，给定坐标 $(x, y)$, 表示撤掉在第 $x$ 行第 $y$ 列的车。数据保障操作之前第 $x$ 行第 $y$ 列一定有车。 - 当 $T = 3$ 时，给定坐标 $(x_1, y_1)$ 与 $(x_2, y_2)$. 问你以 $(x_1, y_1)$ 为左上角, $(x_2, y_2)$ 为右下角的矩形中的所有格子是否全能被棋盘上的车防御。若可以，输出 `Yes`, 否则输出 `No`. 所有数据保证满足 $1 \le x, y \le N, 1 \le x_1 \le x_2 \le N, 1 \le y_1 \le y_2 \le N, 1 \le N \le 10^5, 1 \le Q \le 2 \times 10^5$.

题目描述

You have a square chessboard of size $ n \times n $ . Rows are numbered from top to bottom with numbers from $ 1 $ to $ n $ , and columns — from left to right with numbers from $ 1 $ to $ n $ . So, each cell is denoted with pair of integers $ (x, y) $ ( $ 1 \le x, y \le n $ ), where $ x $ is a row number and $ y $ is a column number. You have to perform $ q $ queries of three types: - Put a new rook in cell $ (x, y) $ . - Remove a rook from cell $ (x, y) $ . It's guaranteed that the rook was put in this cell before. - Check if each cell of subrectangle $ (x_1, y_1) - (x_2, y_2) $ of the board is attacked by at least one rook. Subrectangle is a set of cells $ (x, y) $ such that for each cell two conditions are satisfied: $ x_1 \le x \le x_2 $ and $ y_1 \le y \le y_2 $ . Recall that cell $ (a, b) $ is attacked by a rook placed in cell $ (c, d) $ if either $ a = c $ or $ b = d $ . In particular, the cell containing a rook is attacked by this rook.

输入输出格式

输入格式

The first line contains two integers $ n $ and $ q $ ( $ 1 \le n \le 10^5 $ , $ 1 \le q \le 2 \cdot 10^5 $ ) — the size of the chessboard and the number of queries, respectively. Each of the following $ q $ lines contains description of a query. Description begins with integer $ t $ ( $ t \in \{1, 2, 3\} $ ) which denotes type of a query: - If $ t = 1 $ , two integers $ x $ and $ y $ follows ( $ 1 \le x, y \le n $ ) — coordinated of the cell where the new rook should be put in. It's guaranteed that there is no rook in the cell $ (x, y) $ at the moment of the given query. - If $ t = 2 $ , two integers $ x $ and $ y $ follows ( $ 1 \le x, y \le n $ ) — coordinates of the cell to remove a rook from. It's guaranteed that there is a rook in the cell $ (x, y) $ at the moment of the given query. - If $ t = 3 $ , four integers $ x_1, y_1, x_2 $ and $ y_2 $ follows ( $ 1 \le x_1 \le x_2 \le n $ , $ 1 \le y_1 \le y_2 \le n $ ) — subrectangle to check if each cell of it is attacked by at least one rook. It's guaranteed that among $ q $ queries there is at least one query of the third type.

输出格式

Print the answer for each query of the third type in a separate line. Print "Yes" (without quotes) if each cell of the subrectangle is attacked by at least one rook. Otherwise print "No" (without quotes).

输入输出样例

输入样例 #1

8 10
1 2 4
3 6 2 7 2
1 3 2
3 6 2 7 2
1 4 3
3 2 6 4 8
2 4 3
3 2 6 4 8
1 4 8
3 2 6 4 8

输出样例 #1

No
Yes
Yes
No
Yes

说明

Consider example. After the first two queries the board will look like the following picture (the letter $ R $ denotes cells in which rooks are located, the subrectangle of the query of the third type is highlighted in green): Chessboard after performing the third and the fourth queries: 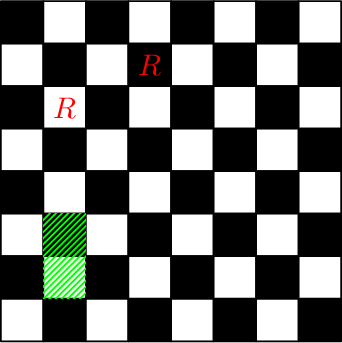Chessboard after performing the fifth and the sixth queries: 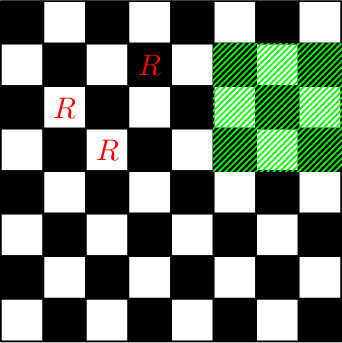Chessboard after performing the seventh and the eighth queries: Chessboard after performing the last two queries: 

**题目大意：**

你有一个 $N \times N$ 的国际象棋棋盘，车可以防御所有同行同列的格子。现在有 $Q$ 次操作或询问，每次给定一个 $T \in \{1, 2, 3\}$，代表操作或询问类型：

- 当 $T = 1$ 时，给定坐标 $(x, y)$，表示在第 $x$ 行第 $y$ 列放置一枚车。
- 当 $T = 2$ 时，给定坐标 $(x, y)$，表示撤掉在第 $x$ 行第 $y$ 列的车。数据保障操作之前第 $x$ 行第 $y$ 列一定有车。
- 当 $T = 3$ 时，给定坐标 $(x_1, y_1)$ 与 $(x_2, y_2)$。问你以 $(x_1, y_1)$ 为左上角，$(x_2, y_2)$ 为右下角的矩形中的所有格子是否全能被棋盘上的车防御。若可以，输出 `Yes`，否则输出 `No`。

所有数据保证满足 $1 \le x, y \le N, 1 \le x_1 \le x_2 \le N, 1 \le y_1 \le y_2 \le N, 1 \le N \le 10^5, 1 \le Q \le 2 \times 10^5$。

**输入输出数据格式：**

**输入格式：**
- 第一行包含两个整数 $n$ 和 $q$（$1 \le n \le 10^5$，$1 \le q \le 2 \cdot 10^5$）—— 棋盘的大小和查询的数量。
- 接下来的 $q$ 行，每行包含一个查询的描述。描述以整数 $t$ 开始（$t \in \{1, 2, 3\}$），表示查询的类型：
- 如果 $t = 1$，后面跟着两个整数 $x$ 和 $y$（$1 \le x, y \le n$）—— 放置新车的单元格坐标。保证在给定查询时单元格 $(x, y)$ 中没有车。
- 如果 $t = 2$，后面跟着两个整数 $x$ 和 $y$（$1 \le x, y \le n$）—— 移除车的单元格坐标。保证在给定查询时单元格 $(x, y)$ 中有车。
- 如果 $t = 3$，后面跟着四个整数 $x_1, y_1, x_2$ 和 $y_2$（$1 \le x_1 \le x_2 \le n$，$1 \le y_1 \le y_2 \le n$）—— 要检查的子矩形，看它是否被至少一辆车攻击。

保证在 $q$ 个查询中至少有一个第三类型的查询。

**输出格式：**
- 对于每个第三类型的查询，在单独的一行中打印答案。如果子矩形中的每个单元格都被至少一辆车攻击，则打印 `Yes`。
- 否则打印 `No`。**题目大意：** 你有一个 $N \times N$ 的国际象棋棋盘，车可以防御所有同行同列的格子。现在有 $Q$ 次操作或询问，每次给定一个 $T \in \{1, 2, 3\}$，代表操作或询问类型： - 当 $T = 1$ 时，给定坐标 $(x, y)$，表示在第 $x$ 行第 $y$ 列放置一枚车。 - 当 $T = 2$ 时，给定坐标 $(x, y)$，表示撤掉在第 $x$ 行第 $y$ 列的车。数据保障操作之前第 $x$ 行第 $y$ 列一定有车。 - 当 $T = 3$ 时，给定坐标 $(x_1, y_1)$ 与 $(x_2, y_2)$。问你以 $(x_1, y_1)$ 为左上角，$(x_2, y_2)$ 为右下角的矩形中的所有格子是否全能被棋盘上的车防御。若可以，输出 `Yes`，否则输出 `No`。 所有数据保证满足 $1 \le x, y \le N, 1 \le x_1 \le x_2 \le N, 1 \le y_1 \le y_2 \le N, 1 \le N \le 10^5, 1 \le Q \le 2 \times 10^5$。 **输入输出数据格式：** **输入格式：** - 第一行包含两个整数 $n$ 和 $q$（$1 \le n \le 10^5$，$1 \le q \le 2 \cdot 10^5$）—— 棋盘的大小和查询的数量。 - 接下来的 $q$ 行，每行包含一个查询的描述。描述以整数 $t$ 开始（$t \in \{1, 2, 3\}$），表示查询的类型： - 如果 $t = 1$，后面跟着两个整数 $x$ 和 $y$（$1 \le x, y \le n$）—— 放置新车的单元格坐标。保证在给定查询时单元格 $(x, y)$ 中没有车。 - 如果 $t = 2$，后面跟着两个整数 $x$ 和 $y$（$1 \le x, y \le n$）—— 移除车的单元格坐标。保证在给定查询时单元格 $(x, y)$ 中有车。 - 如果 $t = 3$，后面跟着四个整数 $x_1, y_1, x_2$ 和 $y_2$（$1 \le x_1 \le x_2 \le n$，$1 \le y_1 \le y_2 \le n$）—— 要检查的子矩形，看它是否被至少一辆车攻击。 保证在 $q$ 个查询中至少有一个第三类型的查询。 **输出格式：** - 对于每个第三类型的查询，在单独的一行中打印答案。如果子矩形中的每个单元格都被至少一辆车攻击，则打印 `Yes`。 - 否则打印 `No`。