Toss a Coin to Your Graph...

题意翻译

珂朵莉给了你一个有向图，边数最大 $ 2×10^5 $ ，每个点有一个点权，任选起点，走k步，问经过的点的最大权值最小能是多少？$ k \leq 10^{18} $，无解输出-1，没有重边和自环，但是会有环。

题目描述

One day Masha was walking in the park and found a graph under a tree... Surprised? Did you think that this problem would have some logical and reasoned story? No way! So, the problem... Masha has an oriented graph which $ i $ -th vertex contains some positive integer $ a_i $ . Initially Masha can put a coin at some vertex. In one operation she can move a coin placed in some vertex $ u $ to any other vertex $ v $ such that there is an oriented edge $ u \to v $ in the graph. Each time when the coin is placed in some vertex $ i $ , Masha write down an integer $ a_i $ in her notebook (in particular, when Masha initially puts a coin at some vertex, she writes an integer written at this vertex in her notebook). Masha wants to make exactly $ k - 1 $ operations in such way that the maximum number written in her notebook is as small as possible.

输入输出格式

输入格式

The first line contains three integers $ n $ , $ m $ and $ k $ ( $ 1 \le n \le 2 \cdot 10^5 $ , $ 0 \le m \le 2 \cdot 10^5 $ , $ 1 \le k \le 10^{18} $ ) — the number of vertices and edges in the graph, and the number of operation that Masha should make. The second line contains $ n $ integers $ a_i $ ( $ 1 \le a_i \le 10^9 $ ) — the numbers written in graph vertices. Each of the following $ m $ lines contains two integers $ u $ and $ v $ ( $ 1 \le u \ne v \le n $ ) — it means that there is an edge $ u \to v $ in the graph. It's guaranteed that graph doesn't contain loops and multi-edges.

输出格式

Print one integer — the minimum value of the maximum number that Masha wrote in her notebook during optimal coin movements. If Masha won't be able to perform $ k - 1 $ operations, print $ -1 $ .

输入输出样例

输入样例 #1

6 7 4
1 10 2 3 4 5
1 2
1 3
3 4
4 5
5 6
6 2
2 5

输出样例 #1

4

输入样例 #2

6 7 100
1 10 2 3 4 5
1 2
1 3
3 4
4 5
5 6
6 2
2 5

输出样例 #2

10

输入样例 #3

2 1 5
1 1
1 2

输出样例 #3

-1

输入样例 #4

1 0 1
1000000000

输出样例 #4

1000000000

说明

Graph described in the first and the second examples is illustrated below. 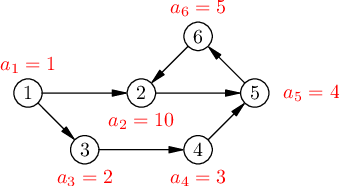In the first example Masha can initially put a coin at vertex $ 1 $ . After that she can perform three operations: $ 1 \to 3 $ , $ 3 \to 4 $ and $ 4 \to 5 $ . Integers $ 1, 2, 3 $ and $ 4 $ will be written in the notepad. In the second example Masha can initially put a coin at vertex $ 2 $ . After that she can perform $ 99 $ operations: $ 2 \to 5 $ , $ 5 \to 6 $ , $ 6 \to 2 $ , $ 2 \to 5 $ , and so on. Integers $ 10, 4, 5, 10, 4, 5, \ldots, 10, 4, 5, 10 $ will be written in the notepad. In the third example Masha won't be able to perform $ 4 $ operations.

**题意翻译**

珂朵莉给了你一个有向图，边数最大 $ 2 \times 10^5 $，每个点有一个点权，任选起点，走k步，问经过的点的最大权值最小能是多少？$ k \leq 10^{18} $，无解输出-1，没有重边和自环，但是会有环。

**题目描述**

玛莎在公园里散步时，在一棵树下发现了一个图...感到惊讶吗？你以为这个问题会有一个合乎逻辑和有道理的故事吗？不可能！所以，问题...

玛莎有一个有向图，第 $ i $ 个顶点包含一些正整数 $ a_i $。最初玛莎可以在某个顶点放一个硬币。在一次操作中，她可以将放在某个顶点 $ u $ 上的硬币移动到图中存在有向边 $ u \to v $ 的任何其他顶点 $ v $。每当硬币放在某个顶点 $ i $ 上时，玛莎就会在她的笔记本上写下整数 $ a_i $（特别是，当玛莎最初在某个顶点放置硬币时，她会写下这个顶点上的整数）。玛莎想进行恰好 $ k - 1 $ 次操作，使得她笔记本上写下的最大数尽可能小。

**输入输出格式**

**输入格式**

第一行包含三个整数 $ n $, $ m $ 和 $ k $ ($ 1 \le n \le 2 \cdot 10^5 $, $ 0 \le m \le 2 \cdot 10^5 $, $ 1 \le k \le 10^{18} $) —— 图中的顶点和边数，以及玛莎应该进行的操作数。

第二行包含 $ n $ 个整数 $ a_i $ ($ 1 \le a_i \le 10^9 $) —— 图顶点上的数字。

接下来的 $ m $ 行每行包含两个整数 $ u $ 和 $ v $ ($ 1 \le u \ne v \le n $) —— 这意味着图中存在一条边 $ u \to v $。

保证图中不包含环和多重边。

**输出格式**

打印一个整数 —— 在最佳硬币移动过程中，玛莎笔记本上写下的最大数的最小值。

如果玛莎不能执行 $ k - 1 $ 操作，打印 $ -1 $。

**输入输出样例**

**输入样例 #1**
```
6 7 4
1 10 2 3 4 5
1 2
1 3
3 4
4 5
5 6
6 2
2 5
```
**输出样例 #1**
```
4
```

**输入样例 #2**
```
6 7 100
1 10 2 3 4 5
1 2
1 3
3 4
4 5
5 6
6 2
2 5
```
**输出样例 #2**
```
10
```

**输入样例 #3**
```
2 1 5
1 1
1 2
```
**输出样例 #3**
```
-1
```

**输入样例 #4**
```
1 0 1
1000000000
```
**输出样例 #4**
```
1000000000
```

**说明**

第一个和第二个例子中描述的图如下所示。


在第一个例子中，玛莎最初可以在顶点 $ 1 $ 放一个硬币。之后她可以进行三次操作：$ 1 \to 3 $, $ 3 \to 4 $ 和 $ 4 \to 5 $。整数 $ 1, 2, 3 $ 和 $ 4 $ 将被写在笔记本上。

在第二个例子中，玛莎最初可以在顶点 $ 2 $ 放一个硬币。之后她可以进行 $ 99 $ 次操作：$ 2 \to 5 $, $ 5 \to 6 $, $ 6 \to 2 $, $ 2 \to 5 $，等等。整数 $ 10, 4, 5, 10, 4, 5, \ldots, 10, 4, 5, 10 $ 将被写在笔记本上。

在第三个例子中，玛莎将无法执行 $ 4 $ 次操作。**题意翻译** 珂朵莉给了你一个有向图，边数最大 $ 2 \times 10^5 $，每个点有一个点权，任选起点，走k步，问经过的点的最大权值最小能是多少？$ k \leq 10^{18} $，无解输出-1，没有重边和自环，但是会有环。 **题目描述** 玛莎在公园里散步时，在一棵树下发现了一个图...感到惊讶吗？你以为这个问题会有一个合乎逻辑和有道理的故事吗？不可能！所以，问题... 玛莎有一个有向图，第 $ i $ 个顶点包含一些正整数 $ a_i $。最初玛莎可以在某个顶点放一个硬币。在一次操作中，她可以将放在某个顶点 $ u $ 上的硬币移动到图中存在有向边 $ u \to v $ 的任何其他顶点 $ v $。每当硬币放在某个顶点 $ i $ 上时，玛莎就会在她的笔记本上写下整数 $ a_i $（特别是，当玛莎最初在某个顶点放置硬币时，她会写下这个顶点上的整数）。玛莎想进行恰好 $ k - 1 $ 次操作，使得她笔记本上写下的最大数尽可能小。 **输入输出格式** **输入格式** 第一行包含三个整数 $ n $, $ m $ 和 $ k $ ($ 1 \le n \le 2 \cdot 10^5 $, $ 0 \le m \le 2 \cdot 10^5 $, $ 1 \le k \le 10^{18} $) —— 图中的顶点和边数，以及玛莎应该进行的操作数。 第二行包含 $ n $ 个整数 $ a_i $ ($ 1 \le a_i \le 10^9 $) —— 图顶点上的数字。 接下来的 $ m $ 行每行包含两个整数 $ u $ 和 $ v $ ($ 1 \le u \ne v \le n $) —— 这意味着图中存在一条边 $ u \to v $。 保证图中不包含环和多重边。 **输出格式** 打印一个整数 —— 在最佳硬币移动过程中，玛莎笔记本上写下的最大数的最小值。 如果玛莎不能执行 $ k - 1 $ 操作，打印 $ -1 $。 **输入输出样例** **输入样例 #1** ``` 6 7 4 1 10 2 3 4 5 1 2 1 3 3 4 4 5 5 6 6 2 2 5 ``` **输出样例 #1** ``` 4 ``` **输入样例 #2** ``` 6 7 100 1 10 2 3 4 5 1 2 1 3 3 4 4 5 5 6 6 2 2 5 ``` **输出样例 #2** ``` 10 ``` **输入样例 #3** ``` 2 1 5 1 1 1 2 ``` **输出样例 #3** ``` -1 ``` **输入样例 #4** ``` 1 0 1 1000000000 ``` **输出样例 #4** ``` 1000000000 ``` **说明** 第一个和第二个例子中描述的图如下所示。  在第一个例子中，玛莎最初可以在顶点 $ 1 $ 放一个硬币。之后她可以进行三次操作：$ 1 \to 3 $, $ 3 \to 4 $ 和 $ 4 \to 5 $。整数 $ 1, 2, 3 $ 和 $ 4 $ 将被写在笔记本上。 在第二个例子中，玛莎最初可以在顶点 $ 2 $ 放一个硬币。之后她可以进行 $ 99 $ 次操作：$ 2 \to 5 $, $ 5 \to 6 $, $ 6 \to 2 $, $ 2 \to 5 $，等等。整数 $ 10, 4, 5, 10, 4, 5, \ldots, 10, 4, 5, 10 $ 将被写在笔记本上。 在第三个例子中，玛莎将无法执行 $ 4 $ 次操作。