Color the Picture

题意翻译

一张图片可分为$n \times m$个格点，每个格点可染上一种颜色。 定义一张美丽的图片为：对于每个格点，**至少**有三个与其**相邻**的格点的颜色与之相同。 注意此处第一行与第$n$行相邻，第一列与第$m$列相邻。 题目将给出$T$组数据。 对于每组数据，第一行为$3$个数$n$，$m$，$k$，为一张空白图片的大小，及能使用的颜色种数。第二行是由$k$个数组成的序列$a$，第$i$个数为第$i$种颜色能使用的次数$a_i$。 对于每组数据，若能将空白图片染成美丽的图片，则输出"Yes"，否则输出"No"。

题目描述

A picture can be represented as an $ n\times m $ grid ( $ n $ rows and $ m $ columns) so that each of the $ n \cdot m $ cells is colored with one color. You have $ k $ pigments of different colors. You have a limited amount of each pigment, more precisely you can color at most $ a_i $ cells with the $ i $ -th pigment. A picture is considered beautiful if each cell has at least $ 3 $ toroidal neighbors with the same color as itself. Two cells are considered toroidal neighbors if they toroidally share an edge. In other words, for some integers $ 1 \leq x_1,x_2 \leq n $ and $ 1 \leq y_1,y_2 \leq m $ , the cell in the $ x_1 $ -th row and $ y_1 $ -th column is a toroidal neighbor of the cell in the $ x_2 $ -th row and $ y_2 $ -th column if one of following two conditions holds: - $ x_1-x_2 \equiv \pm1 \pmod{n} $ and $ y_1=y_2 $ , or - $ y_1-y_2 \equiv \pm1 \pmod{m} $ and $ x_1=x_2 $ . Notice that each cell has exactly $ 4 $ toroidal neighbors. For example, if $ n=3 $ and $ m=4 $ , the toroidal neighbors of the cell $ (1, 2) $ (the cell on the first row and second column) are: $ (3, 2) $ , $ (2, 2) $ , $ (1, 3) $ , $ (1, 1) $ . They are shown in gray on the image below: 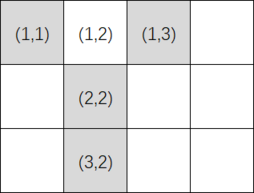The gray cells show toroidal neighbors of $ (1, 2) $ .Is it possible to color all cells with the pigments provided and create a beautiful picture?

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \leq t \leq 10^4 $ ). The description of the test cases follows. The first line of each test case contains three integers $ n $ , $ m $ , and $ k $ ( $ 3 \leq n,m \leq 10^9 $ , $ 1 \leq k \leq 10^5 $ ) — the number of rows and columns of the picture and the number of pigments. The next line contains $ k $ integers $ a_1,a_2,\dots, a_k $ ( $ 1 \leq a_i \leq 10^9 $ ) — $ a_i $ is the maximum number of cells that can be colored with the $ i $ -th pigment. It is guaranteed that the sum of $ k $ over all test cases does not exceed $ 10^5 $ .

输出格式

For each test case, print "Yes" (without quotes) if it is possible to color a beautiful picture. Otherwise, print "No" (without quotes).

输入输出样例

输入样例 #1

6
4 6 3
12 9 8
3 3 2
8 8
3 3 2
9 5
4 5 2
10 11
5 4 2
9 11
10 10 3
11 45 14

输出样例 #1

Yes
No
Yes
Yes
No
No

说明

In the first test case, one possible solution is as follows: In the third test case, we can color all cells with pigment $ 1 $ .

**题目大意：**

题目要求判断是否可以用给定的颜料为一张\( n \times m \)网格的图片染色，使得每个单元格至少有三个与其相邻的单元格颜色相同。相邻指的是在网格世界中，上下边界和左右边界是相连的。给定\( T \)组数据，每组数据包含图片的大小\( n, m \)和颜料种类数\( k \)，以及每种颜料能使用的次数\( a_i \)。对于每组数据，判断是否能染成美丽的图片，如果能则输出"Yes"，否则输出"No"。

**输入输出数据格式：**

**输入格式：**

- 第一行包含一个整数\( t \)（\( 1 \leq t \leq 10^4 \)），表示测试用例的数量。
- 每个测试用例包含两行：
- 第一行包含三个整数\( n, m, k \)（\( 3 \leq n,m \leq 10^9 \), \( 1 \leq k \leq 10^5 \)），分别表示图片的行数、列数和颜料种类数。
- 第二行包含\( k \)个整数\( a_1, a_2, \dots, a_k \)（\( 1 \leq a_i \leq 10^9 \)），表示每种颜料最多可以染的单元格数。

**输出格式：**

- 对于每个测试用例，如果能染成美丽的图片，输出"Yes"，否则输出"No"。**题目大意：** 题目要求判断是否可以用给定的颜料为一张\( n \times m \)网格的图片染色，使得每个单元格至少有三个与其相邻的单元格颜色相同。相邻指的是在网格世界中，上下边界和左右边界是相连的。给定\( T \)组数据，每组数据包含图片的大小\( n, m \)和颜料种类数\( k \)，以及每种颜料能使用的次数\( a_i \)。对于每组数据，判断是否能染成美丽的图片，如果能则输出"Yes"，否则输出"No"。 **输入输出数据格式：** **输入格式：** - 第一行包含一个整数\( t \)（\( 1 \leq t \leq 10^4 \)），表示测试用例的数量。 - 每个测试用例包含两行： - 第一行包含三个整数\( n, m, k \)（\( 3 \leq n,m \leq 10^9 \), \( 1 \leq k \leq 10^5 \)），分别表示图片的行数、列数和颜料种类数。 - 第二行包含\( k \)个整数\( a_1, a_2, \dots, a_k \)（\( 1 \leq a_i \leq 10^9 \)），表示每种颜料最多可以染的单元格数。 **输出格式：** - 对于每个测试用例，如果能染成美丽的图片，输出"Yes"，否则输出"No"。