Rain

题意翻译

给定一个 $ n $ ，这 $ n $ 天会降雨，每一个降雨天有一个 $ x_i $ 和一个 $ p_i $ ，表示以 $ x_i $ 为中心，降雨量向左右两边递减，即对于所有的数轴上的点 $ x $ ,其降雨量都会增加 $ max(0,p_i−∣x_i−x∣) $ 现在你可以消除一天的降雨，问消除第 $ i $ 天的降雨是否可以使得没有任何地方的降雨大于 $ m $

题目描述

You are the owner of a harvesting field which can be modeled as an infinite line, whose positions are identified by integers. It will rain for the next $ n $ days. On the $ i $ -th day, the rain will be centered at position $ x_i $ and it will have intensity $ p_i $ . Due to these rains, some rainfall will accumulate; let $ a_j $ be the amount of rainfall accumulated at integer position $ j $ . Initially $ a_j $ is $ 0 $ , and it will increase by $ \max(0,p_i-|x_i-j|) $ after the $ i $ -th day's rain. A flood will hit your field if, at any moment, there is a position $ j $ with accumulated rainfall $ a_j>m $ . You can use a magical spell to erase exactly one day's rain, i.e., setting $ p_i=0 $ . For each $ i $ from $ 1 $ to $ n $ , check whether in case of erasing the $ i $ -th day's rain there is no flood.

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \leq t \leq 10^4 $ ). The description of the test cases follows. The first line of each test case contains two integers $ n $ and $ m $ ( $ 1 \leq n \leq 2 \cdot 10^5 $ , $ 1 \leq m \leq 10^9 $ ) — the number of rainy days and the maximal accumulated rainfall with no flood occurring. Then $ n $ lines follow. The $ i $ -th of these lines contains two integers $ x_i $ and $ p_i $ ( $ 1 \leq x_i,p_i \leq 10^9 $ ) — the position and intensity of the $ i $ -th day's rain. The sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

输出格式

For each test case, output a binary string $ s $ length of $ n $ . The $ i $ -th character of $ s $ is 1 if after erasing the $ i $ -th day's rain there is no flood, while it is 0, if after erasing the $ i $ -th day's rain the flood still happens.

输入输出样例

输入样例 #1

4
3 6
1 5
5 5
3 4
2 3
1 3
5 2
2 5
1 6
10 6
6 12
4 5
1 6
12 5
5 5
9 7
8 3

输出样例 #1

001
11
00
100110

说明

In the first test case, if we do not use the spell, the accumulated rainfall distribution will be like this: 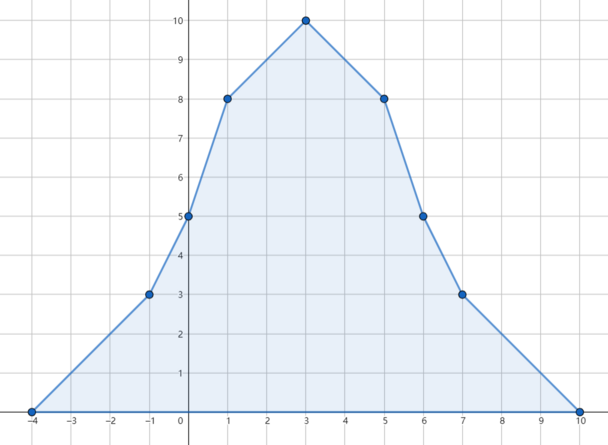If we erase the third day's rain, the flood is avoided and the accumulated rainfall distribution looks like this: 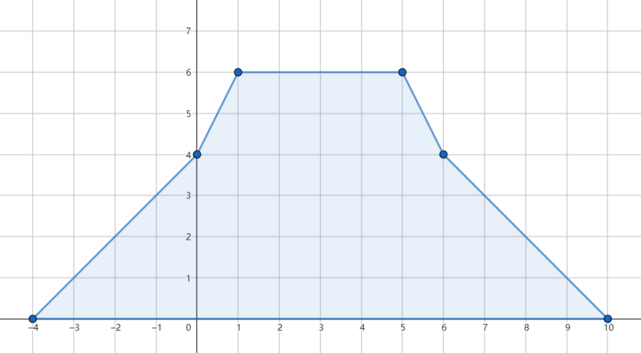In the second test case, since initially the flood will not happen, we can erase any day's rain. In the third test case, there is no way to avoid the flood.

**题目大意：**

有一个可以视为无限长直线的田野，其位置由整数标识。在接下来的 $ n $ 天里，每天都会下雨。第 $ i $ 天的雨会以位置 $ x_i $ 为中心，强度为 $ p_i $ 。由于这些降雨，一些地方会有积水累积；用 $ a_j $ 表示在整数位置 $ j $ 累积的降雨量。最初 $ a_j $ 为 0，在第 $ i $ 天降雨后，它会增加 $ \max(0,p_i-|x_i-j|) $。

如果任何时候有一个位置 $ j $ 的累积降雨量 $ a_j>m $，就会发生洪水。

你可以使用一个魔法咒语来消除恰好一天的雨，即设置 $ p_i=0 $。对于每个 $ i $ 从 1 到 $ n $，检查是否在消除第 $ i $ 天的雨之后不会发生洪水。

**输入输出数据格式：**

**输入格式：**

每个测试包含多个测试案例。第一行包含测试案例的数量 $ t $（$ 1 \leq t \leq 10^4 $）。接下来是测试案例的描述。

每个测试案例的第一行包含两个整数 $ n $ 和 $ m $（$ 1 \leq n \leq 2 \cdot 10^5 $，$ 1 \leq m \leq 10^9 $）——雨天的数量和没有发生洪水时的最大累积降雨量。

然后是 $ n $ 行。第 $ i $ 行包含两个整数 $ x_i $ 和 $ p_i $（$ 1 \leq x_i,p_i \leq 10^9 $）——第 $ i $ 天降雨的位置和强度。

所有测试案例中 $ n $ 的总和不超过 $ 2 \cdot 10^5 $。

**输出格式：**

对于每个测试案例，输出一个长度为 $ n $ 的二进制字符串 $ s $。如果消除第 $ i $ 天的雨之后没有发生洪水，那么 $ s $ 的第 $ i $ 个字符是 1；如果消除第 $ i $ 天的雨之后仍然发生洪水，则为 0。**题目大意：** 有一个可以视为无限长直线的田野，其位置由整数标识。在接下来的 $ n $ 天里，每天都会下雨。第 $ i $ 天的雨会以位置 $ x_i $ 为中心，强度为 $ p_i $ 。由于这些降雨，一些地方会有积水累积；用 $ a_j $ 表示在整数位置 $ j $ 累积的降雨量。最初 $ a_j $ 为 0，在第 $ i $ 天降雨后，它会增加 $ \max(0,p_i-|x_i-j|) $。 如果任何时候有一个位置 $ j $ 的累积降雨量 $ a_j>m $，就会发生洪水。 你可以使用一个魔法咒语来消除恰好一天的雨，即设置 $ p_i=0 $。对于每个 $ i $ 从 1 到 $ n $，检查是否在消除第 $ i $ 天的雨之后不会发生洪水。 **输入输出数据格式：** **输入格式：** 每个测试包含多个测试案例。第一行包含测试案例的数量 $ t $（$ 1 \leq t \leq 10^4 $）。接下来是测试案例的描述。 每个测试案例的第一行包含两个整数 $ n $ 和 $ m $（$ 1 \leq n \leq 2 \cdot 10^5 $，$ 1 \leq m \leq 10^9 $）——雨天的数量和没有发生洪水时的最大累积降雨量。 然后是 $ n $ 行。第 $ i $ 行包含两个整数 $ x_i $ 和 $ p_i $（$ 1 \leq x_i,p_i \leq 10^9 $）——第 $ i $ 天降雨的位置和强度。 所有测试案例中 $ n $ 的总和不超过 $ 2 \cdot 10^5 $。 **输出格式：** 对于每个测试案例，输出一个长度为 $ n $ 的二进制字符串 $ s $。如果消除第 $ i $ 天的雨之后没有发生洪水，那么 $ s $ 的第 $ i $ 个字符是 1；如果消除第 $ i $ 天的雨之后仍然发生洪水，则为 0。