Madoka and The Corruption Scheme

题意翻译

有$2^n$名参赛者，参赛者编号为$1$至$2^n$。 一共有$n$轮比赛，每一轮，参赛者两两比赛，胜者进入下一轮。因此如图所示，赛程图是一个满二叉树。 现在你可以决定每一个参赛者第一轮的初始排列顺序（对应二叉树叶子节点的顺序），并且你可以决定每一场比赛是左边的人胜出或是右边的人胜出（如图红线为胜出者）。你希望第一名的人编号最小。 但是，有另一个人也能操纵比赛。他可以更改任意$k$场比赛的结果。 输出你能确保得第一名的人的编号的最小值，对$10^9+7$取模。

题目描述

Madoka decided to entrust the organization of a major computer game tournament "OSU"! In this tournament, matches are held according to the "Olympic system". In other words, there are $ 2^n $ participants in the tournament, numbered with integers from $ 1 $ to $ 2^n $ . There are $ n $ rounds in total in the tournament. In the $ i $ -th round there are $ 2^{n - i} $ matches between two players (one of whom is right, the other is left), after which the winners go further along the tournament grid, and the losing participants are eliminated from the tournament. Herewith, the relative order in the next round does not change. And the winner of the tournament — is the last remaining participant. But the smaller the participant's number, the more he will pay Madoka if he wins, so Madoka wants the participant with the lowest number to win. To do this, she can arrange the participants in the first round as she likes, and also determine for each match who will win — the participant on the left or right. But Madoka knows that tournament sponsors can change the winner in matches no more than $ k $ times. (That is, if the participant on the left won before the change, then the participant on the right will win after the change, and if the participant on the right won, then the participant on the left will win after the change). 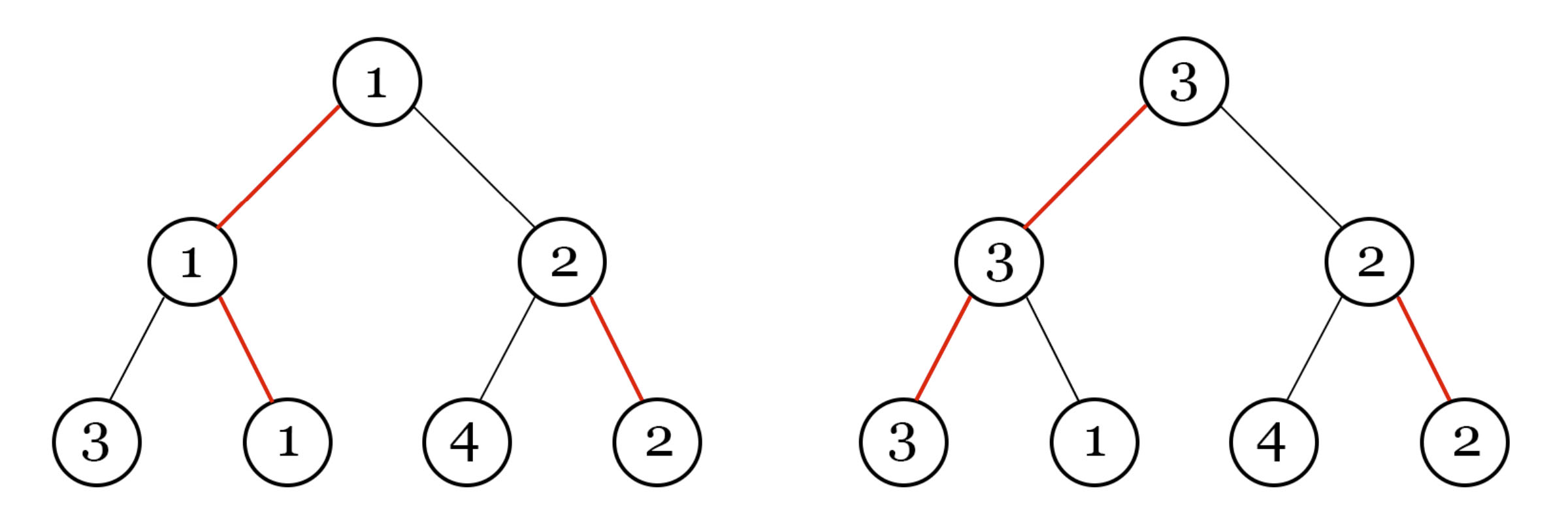So, the first image shows the tournament grid that Madoka made, where the red lines denote who should win the match. And the second one shows the tournament grid, after one change in the outcome of the match by sponsors (a match between $ 1 $ and $ 3 $ players).Print the minimum possible number of the winner in the tournament, which Madoka can get regardless of changes in sponsors. But since the answer can be very large, output it modulo $ 10^9 + 7 $ . Note that we need to minimize the answer, and only then take it modulo.

输入输出格式

输入格式

The first and the only line contains two integers $ n $ and $ k $ ( $ 1 \le n \le 10^5, 1 \le k \le \min(2^n - 1, 10^9) $ ) — the number of rounds in the tournament and the number of outcomes that sponsors can change.

输出格式

Print exactly one integer — the minimum number of the winner modulo $ 10^9 + 7 $

输入输出样例

输入样例 #1

1 1

输出样例 #1

2

输入样例 #2

2 1

输出样例 #2

3

输入样例 #3

3 2

输出样例 #3

7

说明

In the first example, there is only one match between players $ 1 $ and $ 2 $ , so the sponsors can always make player $ 2 $ wins. The tournament grid from the second example is shown in the picture in the statement.

**题目大意：**
在“OSU”计算机游戏大赛中，有\(2^n\)名参赛者，编号从1到\(2^n\)。总共有\(n\)轮比赛，每一轮，参赛者两两对决，胜者晋级下一轮。你可以决定第一轮的初始排列顺序以及每一场比赛的胜者。但还有另一个人可以更改任意\(k\)场比赛的结果。你需要输出能确保得第一名的人的编号的最小值，对\(10^9+7\)取模。

**输入输出数据格式：**
- **输入格式：** 第一行包含两个整数\(n\)和\(k\)（\(1 \le n \le 10^5, 1 \le k \le \min(2^n - 1, 10^9)\)），分别表示比赛轮数和赞助商可以更改的比赛结果数量。
- **输出格式：** 输出一个整数，即Madoka可以确保的最小可能获胜者编号，对\(10^9+7\)取模。

**输入输出样例：**
- **输入样例 #1：**
```
1 1
```
- **输出样例 #1：**
```
2
```
- **输入样例 #2：**
```
2 1
```
- **输出样例 #2：**
```
3
```
- **输入样例 #3：**
```
3 2
```
- **输出样例 #3：**
```
7
\]**题目大意：** 在“OSU”计算机游戏大赛中，有\(2^n\)名参赛者，编号从1到\(2^n\)。总共有\(n\)轮比赛，每一轮，参赛者两两对决，胜者晋级下一轮。你可以决定第一轮的初始排列顺序以及每一场比赛的胜者。但还有另一个人可以更改任意\(k\)场比赛的结果。你需要输出能确保得第一名的人的编号的最小值，对\(10^9+7\)取模。 **输入输出数据格式：** - **输入格式：** 第一行包含两个整数\(n\)和\(k\)（\(1 \le n \le 10^5, 1 \le k \le \min(2^n - 1, 10^9)\)），分别表示比赛轮数和赞助商可以更改的比赛结果数量。 - **输出格式：** 输出一个整数，即Madoka可以确保的最小可能获胜者编号，对\(10^9+7\)取模。 **输入输出样例：** - **输入样例 #1：** ``` 1 1 ``` - **输出样例 #1：** ``` 2 ``` - **输入样例 #2：** ``` 2 1 ``` - **输出样例 #2：** ``` 3 ``` - **输入样例 #3：** ``` 3 2 ``` - **输出样例 #3：** ``` 7 \]