309786: CF1735E. House Planning
Memory Limit:256 MB
Time Limit:3 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
House Planning
题意翻译
在一个数轴上有 $n$ 幢楼房,你在两个地方 $p_1,p_2$ 观测它们到你所在位置的的距离。在 $p_1$ 处得到了 $d_1$,在 $p_2$ 处得到了 $d_2$,其中 $d_{i,j}$ 表示在 $p_i$ 处距楼房 $a_j$ 的距离。 不幸的是,你非常粗心地把 $d_i$ 打乱了(即 $d_1,d_2$ 无序,$d_1,d_2$ 间不会交换元素)。所以请尝试根据给定的 $d_1,d_2$ 求出一组合法的 $p_1,p_2,a$。无解输出 `NO`。题目描述
There are $ n $ houses in your city arranged on an axis at points $ h_1, h_2, \ldots, h_n $ . You want to build a new house for yourself and consider two options where to place it: points $ p_1 $ and $ p_2 $ . As you like visiting friends, you have calculated in advance the distances from both options to all existing houses. More formally, you have calculated two arrays $ d_1 $ , $ d_2 $ : $ d_{i, j} = \left|p_i - h_j\right| $ , where $ |x| $ defines the absolute value of $ x $ . After a long time of inactivity you have forgotten the locations of the houses $ h $ and the options $ p_1 $ , $ p_2 $ . But your diary still keeps two arrays — $ d_1 $ , $ d_2 $ , whose authenticity you doubt. Also, the values inside each array could be shuffled, so values at the same positions of $ d_1 $ and $ d_2 $ may correspond to different houses. Pay attention, that values from one array could not get to another, in other words, all values in the array $ d_1 $ correspond the distances from $ p_1 $ to the houses, and in the array $ d_2 $ — from $ p_2 $ to the houses. Also pay attention, that the locations of the houses $ h_i $ and the considered options $ p_j $ could match. For example, the next locations are correct: $ h = \{1, 0, 3, 3\} $ , $ p = \{1, 1\} $ , that could correspond to already shuffled $ d_1 = \{0, 2, 1, 2\} $ , $ d_2 = \{2, 2, 1, 0\} $ . Check whether there are locations of houses $ h $ and considered points $ p_1 $ , $ p_2 $ , for which the founded arrays of distances would be correct. If it is possible, find appropriate locations of houses and considered options.输入输出格式
输入格式
The first line of the input contains a single integer $ t $ ( $ 1 \le t \le 10^3 $ ) — the number of test cases. The description of test cases follows. The first line of each test case contains one integer $ n $ ( $ 1 \le n \le 10^3 $ ) — the length of arrays $ d_1 $ , $ d_2 $ . The next two lines contain $ n $ integers each: arrays $ d_1 $ and $ d_2 $ ( $ 0 \le d_{i, j} \le 10^9 $ ) respectively. It is guaranteed that the sum of $ n $ over all test cases doesn't exceed $ 2 \cdot 10^3 $ .
输出格式
For each test case, output a single line "NO" if there is no answer. Otherwise output three lines. The first line must contain "YES". In the second line, print $ n $ integers $ h_1, h_2, \ldots, h_n $ . In the third line print two integers $ p_1 $ , $ p_2 $ . It must be satisfied that $ 0 \le h_i, p_1, p_2 \le 2 \cdot 10^9 $ . We can show that if there is an answer, then there is one satisfying these constraints. If there are several answers, output any of them.
输入输出样例
输入样例 #1
4
1
5
5
2
10 12
5 20
2
10 33
26 69
4
0 2 1 2
2 2 1 0输出样例 #1
YES
5
0 10
NO
YES
0 43
33 69
YES
1 0 3 3
1 1说明
In the image below you can see the sample solutions. Planned houses are shown in bright colours: pink and purple. Existing houses are dim. In test case $ 1 $ , the first planned house is located at point $ 0 $ , the second at point $ 10 $ . The existing house is located at point $ 5 $ and is at a distance of $ 5 $ from both planned houses. It can be shown that there is no answer for test case $ 2 $ . In test case $ 3 $ , the planned houses are located at points $ 33 $ and $ 69 $ . Note that in test case $ 4 $ , both plans are located at point $ 1 $ , where one of the existing houses is located at the same time. It is a correct placement. 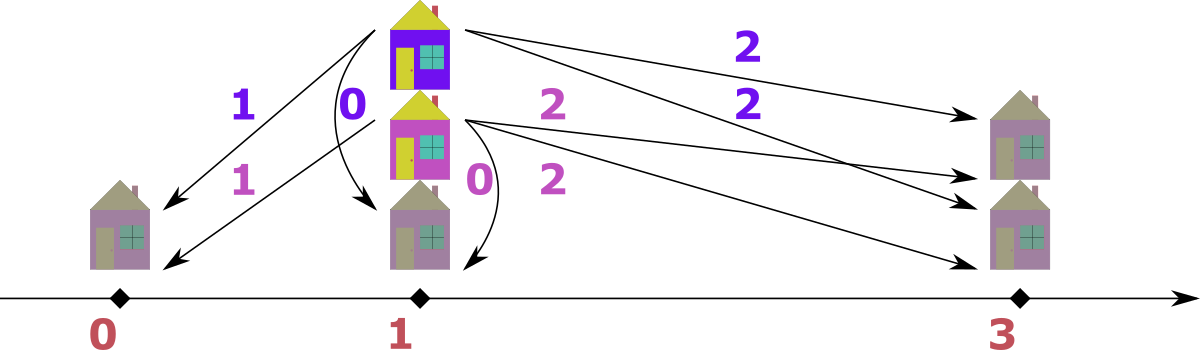Input
题意翻译
在一个数轴上有 $n$ 幢楼房,你在两个地方 $p_1,p_2$ 观测它们到你所在位置的的距离。在 $p_1$ 处得到了 $d_1$,在 $p_2$ 处得到了 $d_2$,其中 $d_{i,j}$ 表示在 $p_i$ 处距楼房 $a_j$ 的距离。 不幸的是,你非常粗心地把 $d_i$ 打乱了(即 $d_1,d_2$ 无序,$d_1,d_2$ 间不会交换元素)。所以请尝试根据给定的 $d_1,d_2$ 求出一组合法的 $p_1,p_2,a$。无解输出 `NO`。Output
**房屋规划**
**题意翻译:**
在数轴上有n幢楼房,你在两个位置p1,p2观测它们到你所在位置的距离。在p1处得到了d1,在p2处得到了d2,其中di,j表示在pi处距楼房aj的距离。
不幸的是,你非常粗心地把di打乱了(即d1,d2无序,d1,d2间不会交换元素)。所以请尝试根据给定的d1,d2求出一组合法的p1,p2,a。无解输出`NO`。
**题目描述:**
你的城市里有一条轴上有n幢房子,分别位于点h1, h2, ..., hn。你想为自己建一座新房子,并考虑两个位置:点p1和p2。
因为你喜欢拜访朋友,所以你已经提前计算了两个位置到所有现有房子的距离。更正式地说,你已经计算了两个数组d1, d2:di,j = |pi - hj|,其中|x|定义了x的绝对值。
在长时间的闲置之后,你已经忘记了房子的位置h以及选项p1, p2。但你的日记仍然保存着两个数组——d1, d2,你对它们的真实性表示怀疑。同时,每个数组内的值可能被随机排列,所以d1和d2相同位置的值可能对应不同的房子。请注意,一个数组中的值不会跑到另一个数组中,换句话说,数组d1中的所有值都对应于从p1到房子的距离,在数组d2中——从p2到房子的距离。
还要注意,房子的位置hi和考虑的选项pj可能相同。例如,以下位置是正确的:h = {1, 0, 3, 3},p = {1, 1},可能对应于已经打乱的d1 = {0, 2, 1, 2},d2 = {2, 2, 1, 0}。
检查是否存在房子的位置h和考虑的点p1, p2,使得找到的距离数组是正确的。如果可能,找到合适的房子位置和考虑的选项。
**输入输出格式:**
**输入格式:**
输入的第一行包含一个整数t(1≤t≤10^3)——测试用例的数量。接下来是测试用例的描述。
每个测试用例的第一行包含一个整数n(1≤n≤10^3)——数组d1, d2的长度。
接下来两行各包含n个整数:数组d1和d2(0≤di,j≤10^9)。
保证所有测试用例的n之和不超过2×10^3。
**输出格式:**
对于每个测试用例,如果没有答案,则输出一行"NO"。
否则,输出三行。第一行必须包含"YES"。在第二行,打印n个整数h1, h2, ..., hn。在第三行打印两个整数p1, p2。
必须满足0≤hi, p1, p2≤2×10^9。我们可以证明,如果存在答案,则存在一个满足这些约束的答案。
如果存在多个答案,输出其中任何一个。
**输入输出样例:**
**输入样例 #1:**
```
4
1
5
5
2
10 12
5 20
2
10 33
26 69
4
0 2 1 2
2 2 1 0
```
**输出样例 #1:**
```
YES
5
0 10
NO
YES
0 43
33 69
YES
1 0 3 3
1 1
```
**说明:**
在下面的图片中,你可以看到样本解决方案。规划中的房子用鲜艳的颜色显示:粉红色和紫色。现有的房子颜色较暗。
在测试用例1中,第一个规划中的房子位于点0,第二个位于点10。现有的房子位于点5,并且距离两个规划中的房子各5个单位。
可以证明测试用例2没有答案。
在测试用例3中,规划中的房子位于点33和69。
请注意,在测试用例4中,两个规划都位于点1,其中一个现有的房子同时位于该点。这是一个正确的放置。**房屋规划** **题意翻译:** 在数轴上有n幢楼房,你在两个位置p1,p2观测它们到你所在位置的距离。在p1处得到了d1,在p2处得到了d2,其中di,j表示在pi处距楼房aj的距离。 不幸的是,你非常粗心地把di打乱了(即d1,d2无序,d1,d2间不会交换元素)。所以请尝试根据给定的d1,d2求出一组合法的p1,p2,a。无解输出`NO`。 **题目描述:** 你的城市里有一条轴上有n幢房子,分别位于点h1, h2, ..., hn。你想为自己建一座新房子,并考虑两个位置:点p1和p2。 因为你喜欢拜访朋友,所以你已经提前计算了两个位置到所有现有房子的距离。更正式地说,你已经计算了两个数组d1, d2:di,j = |pi - hj|,其中|x|定义了x的绝对值。 在长时间的闲置之后,你已经忘记了房子的位置h以及选项p1, p2。但你的日记仍然保存着两个数组——d1, d2,你对它们的真实性表示怀疑。同时,每个数组内的值可能被随机排列,所以d1和d2相同位置的值可能对应不同的房子。请注意,一个数组中的值不会跑到另一个数组中,换句话说,数组d1中的所有值都对应于从p1到房子的距离,在数组d2中——从p2到房子的距离。 还要注意,房子的位置hi和考虑的选项pj可能相同。例如,以下位置是正确的:h = {1, 0, 3, 3},p = {1, 1},可能对应于已经打乱的d1 = {0, 2, 1, 2},d2 = {2, 2, 1, 0}。 检查是否存在房子的位置h和考虑的点p1, p2,使得找到的距离数组是正确的。如果可能,找到合适的房子位置和考虑的选项。 **输入输出格式:** **输入格式:** 输入的第一行包含一个整数t(1≤t≤10^3)——测试用例的数量。接下来是测试用例的描述。 每个测试用例的第一行包含一个整数n(1≤n≤10^3)——数组d1, d2的长度。 接下来两行各包含n个整数:数组d1和d2(0≤di,j≤10^9)。 保证所有测试用例的n之和不超过2×10^3。 **输出格式:** 对于每个测试用例,如果没有答案,则输出一行"NO"。 否则,输出三行。第一行必须包含"YES"。在第二行,打印n个整数h1, h2, ..., hn。在第三行打印两个整数p1, p2。 必须满足0≤hi, p1, p2≤2×10^9。我们可以证明,如果存在答案,则存在一个满足这些约束的答案。 如果存在多个答案,输出其中任何一个。 **输入输出样例:** **输入样例 #1:** ``` 4 1 5 5 2 10 12 5 20 2 10 33 26 69 4 0 2 1 2 2 2 1 0 ``` **输出样例 #1:** ``` YES 5 0 10 NO YES 0 43 33 69 YES 1 0 3 3 1 1 ``` **说明:** 在下面的图片中,你可以看到样本解决方案。规划中的房子用鲜艳的颜色显示:粉红色和紫色。现有的房子颜色较暗。 在测试用例1中,第一个规划中的房子位于点0,第二个位于点10。现有的房子位于点5,并且距离两个规划中的房子各5个单位。 可以证明测试用例2没有答案。 在测试用例3中,规划中的房子位于点33和69。 请注意,在测试用例4中,两个规划都位于点1,其中一个现有的房子同时位于该点。这是一个正确的放置。
**题意翻译:**
在数轴上有n幢楼房,你在两个位置p1,p2观测它们到你所在位置的距离。在p1处得到了d1,在p2处得到了d2,其中di,j表示在pi处距楼房aj的距离。
不幸的是,你非常粗心地把di打乱了(即d1,d2无序,d1,d2间不会交换元素)。所以请尝试根据给定的d1,d2求出一组合法的p1,p2,a。无解输出`NO`。
**题目描述:**
你的城市里有一条轴上有n幢房子,分别位于点h1, h2, ..., hn。你想为自己建一座新房子,并考虑两个位置:点p1和p2。
因为你喜欢拜访朋友,所以你已经提前计算了两个位置到所有现有房子的距离。更正式地说,你已经计算了两个数组d1, d2:di,j = |pi - hj|,其中|x|定义了x的绝对值。
在长时间的闲置之后,你已经忘记了房子的位置h以及选项p1, p2。但你的日记仍然保存着两个数组——d1, d2,你对它们的真实性表示怀疑。同时,每个数组内的值可能被随机排列,所以d1和d2相同位置的值可能对应不同的房子。请注意,一个数组中的值不会跑到另一个数组中,换句话说,数组d1中的所有值都对应于从p1到房子的距离,在数组d2中——从p2到房子的距离。
还要注意,房子的位置hi和考虑的选项pj可能相同。例如,以下位置是正确的:h = {1, 0, 3, 3},p = {1, 1},可能对应于已经打乱的d1 = {0, 2, 1, 2},d2 = {2, 2, 1, 0}。
检查是否存在房子的位置h和考虑的点p1, p2,使得找到的距离数组是正确的。如果可能,找到合适的房子位置和考虑的选项。
**输入输出格式:**
**输入格式:**
输入的第一行包含一个整数t(1≤t≤10^3)——测试用例的数量。接下来是测试用例的描述。
每个测试用例的第一行包含一个整数n(1≤n≤10^3)——数组d1, d2的长度。
接下来两行各包含n个整数:数组d1和d2(0≤di,j≤10^9)。
保证所有测试用例的n之和不超过2×10^3。
**输出格式:**
对于每个测试用例,如果没有答案,则输出一行"NO"。
否则,输出三行。第一行必须包含"YES"。在第二行,打印n个整数h1, h2, ..., hn。在第三行打印两个整数p1, p2。
必须满足0≤hi, p1, p2≤2×10^9。我们可以证明,如果存在答案,则存在一个满足这些约束的答案。
如果存在多个答案,输出其中任何一个。
**输入输出样例:**
**输入样例 #1:**
```
4
1
5
5
2
10 12
5 20
2
10 33
26 69
4
0 2 1 2
2 2 1 0
```
**输出样例 #1:**
```
YES
5
0 10
NO
YES
0 43
33 69
YES
1 0 3 3
1 1
```
**说明:**
在下面的图片中,你可以看到样本解决方案。规划中的房子用鲜艳的颜色显示:粉红色和紫色。现有的房子颜色较暗。
在测试用例1中,第一个规划中的房子位于点0,第二个位于点10。现有的房子位于点5,并且距离两个规划中的房子各5个单位。
可以证明测试用例2没有答案。
在测试用例3中,规划中的房子位于点33和69。
请注意,在测试用例4中,两个规划都位于点1,其中一个现有的房子同时位于该点。这是一个正确的放置。**房屋规划** **题意翻译:** 在数轴上有n幢楼房,你在两个位置p1,p2观测它们到你所在位置的距离。在p1处得到了d1,在p2处得到了d2,其中di,j表示在pi处距楼房aj的距离。 不幸的是,你非常粗心地把di打乱了(即d1,d2无序,d1,d2间不会交换元素)。所以请尝试根据给定的d1,d2求出一组合法的p1,p2,a。无解输出`NO`。 **题目描述:** 你的城市里有一条轴上有n幢房子,分别位于点h1, h2, ..., hn。你想为自己建一座新房子,并考虑两个位置:点p1和p2。 因为你喜欢拜访朋友,所以你已经提前计算了两个位置到所有现有房子的距离。更正式地说,你已经计算了两个数组d1, d2:di,j = |pi - hj|,其中|x|定义了x的绝对值。 在长时间的闲置之后,你已经忘记了房子的位置h以及选项p1, p2。但你的日记仍然保存着两个数组——d1, d2,你对它们的真实性表示怀疑。同时,每个数组内的值可能被随机排列,所以d1和d2相同位置的值可能对应不同的房子。请注意,一个数组中的值不会跑到另一个数组中,换句话说,数组d1中的所有值都对应于从p1到房子的距离,在数组d2中——从p2到房子的距离。 还要注意,房子的位置hi和考虑的选项pj可能相同。例如,以下位置是正确的:h = {1, 0, 3, 3},p = {1, 1},可能对应于已经打乱的d1 = {0, 2, 1, 2},d2 = {2, 2, 1, 0}。 检查是否存在房子的位置h和考虑的点p1, p2,使得找到的距离数组是正确的。如果可能,找到合适的房子位置和考虑的选项。 **输入输出格式:** **输入格式:** 输入的第一行包含一个整数t(1≤t≤10^3)——测试用例的数量。接下来是测试用例的描述。 每个测试用例的第一行包含一个整数n(1≤n≤10^3)——数组d1, d2的长度。 接下来两行各包含n个整数:数组d1和d2(0≤di,j≤10^9)。 保证所有测试用例的n之和不超过2×10^3。 **输出格式:** 对于每个测试用例,如果没有答案,则输出一行"NO"。 否则,输出三行。第一行必须包含"YES"。在第二行,打印n个整数h1, h2, ..., hn。在第三行打印两个整数p1, p2。 必须满足0≤hi, p1, p2≤2×10^9。我们可以证明,如果存在答案,则存在一个满足这些约束的答案。 如果存在多个答案,输出其中任何一个。 **输入输出样例:** **输入样例 #1:** ``` 4 1 5 5 2 10 12 5 20 2 10 33 26 69 4 0 2 1 2 2 2 1 0 ``` **输出样例 #1:** ``` YES 5 0 10 NO YES 0 43 33 69 YES 1 0 3 3 1 1 ``` **说明:** 在下面的图片中,你可以看到样本解决方案。规划中的房子用鲜艳的颜色显示:粉红色和紫色。现有的房子颜色较暗。 在测试用例1中,第一个规划中的房子位于点0,第二个位于点10。现有的房子位于点5,并且距离两个规划中的房子各5个单位。 可以证明测试用例2没有答案。 在测试用例3中,规划中的房子位于点33和69。 请注意,在测试用例4中,两个规划都位于点1,其中一个现有的房子同时位于该点。这是一个正确的放置。