309951: CF1764D. Doremy's Pegging Game
Memory Limit:512 MB
Time Limit:1 S
Judge Style:Text Compare
Creator:
Submit:0
Solved:0
Description
Doremy's Pegging Game
题意翻译
现在有 $n+1$ 个钉子。有红色钉子 $n$ 个,他们如图所示排列成一个正 $n$ 边形,他们逆时针从 $1$ 到 $n$ 进行标号,他们分别代表正 $n$ 边形的顶点。有一个蓝色钉子在正 $n$ 边形的正中间,如图所示。现在还有一个橡皮筋将 $n$ 个顶点围住,形成一个正 $n$ 边形的轮廓如图所示。  现在有一个空序列 $a$,在橡皮筋没有碰到蓝色钉子之前你可以执行以下操作: - 选择一个编号为 $x$ 的钉子并且这个钉子并没有被消除。 - 将这个钉子给消除并且将 $x$ 加入到 $a$ 中。 你需要计算出最终可以得到多少种不同的 $a$,这个结果很大,你只需要输出他对 $p$ 进行取模的值,保证 $p$ 是一个素数。题目描述
Doremy has $ n+1 $ pegs. There are $ n $ red pegs arranged as vertices of a regular $ n $ -sided polygon, numbered from $ 1 $ to $ n $ in anti-clockwise order. There is also a blue peg of slightly smaller diameter in the middle of the polygon. A rubber band is stretched around the red pegs. Doremy is very bored today and has decided to play a game. Initially, she has an empty array $ a $ . While the rubber band does not touch the blue peg, she will: 1. choose $ i $ ( $ 1 \leq i \leq n $ ) such that the red peg $ i $ has not been removed; 2. remove the red peg $ i $ ; 3. append $ i $ to the back of $ a $ . Doremy wonders how many possible different arrays $ a $ can be produced by the following process. Since the answer can be big, you are only required to output it modulo $ p $ . $ p $ is guaranteed to be a prime number. 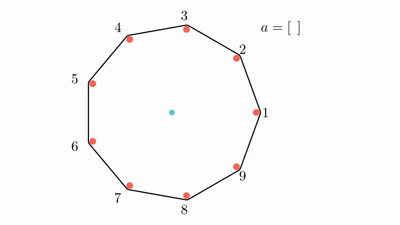 game with $ n=9 $ and $ a=[7,5,2,8,3,9,4] $ and another game with $ n=8 $ and $ a=[3,4,7,1,8,5,2] $输入输出格式
输入格式
The first line contains two integers $ n $ and $ p $ ( $ 3 \leq n \leq 5000 $ , $ 10^8 \le p \le 10^9 $ ) — the number of red pegs and the modulo respectively. $ p $ is guaranteed to be a prime number.
输出格式
Output a single integer, the number of different arrays $ a $ that can be produced by the process described above modulo $ p $ .
输入输出样例
输入样例 #1
4 100000007输出样例 #1
16输入样例 #2
1145 141919831输出样例 #2
105242108说明
In the first test case, $ n=4 $ , some possible arrays $ a $ that can be produced are $ [4,2,3] $ and $ [1,4] $ . However, it is not possible for $ a $ to be $ [1] $ or $ [1,4,3] $ .Input
题意翻译
现在有 $n+1$ 个钉子。有红色钉子 $n$ 个,他们如图所示排列成一个正 $n$ 边形,他们逆时针从 $1$ 到 $n$ 进行标号,他们分别代表正 $n$ 边形的顶点。有一个蓝色钉子在正 $n$ 边形的正中间,如图所示。现在还有一个橡皮筋将 $n$ 个顶点围住,形成一个正 $n$ 边形的轮廓如图所示。  现在有一个空序列 $a$,在橡皮筋没有碰到蓝色钉子之前你可以执行以下操作: - 选择一个编号为 $x$ 的钉子并且这个钉子并没有被消除。 - 将这个钉子给消除并且将 $x$ 加入到 $a$ 中。 你需要计算出最终可以得到多少种不同的 $a$,这个结果很大,你只需要输出他对 $p$ 进行取模的值,保证 $p$ 是一个素数。Output
**题意翻译**
现在有 $n+1$ 个钉子。有红色钉子 $n$ 个,它们如图所示排列成一个正 $n$ 边形,它们逆时针从 $1$ 到 $n$ 进行标号,它们分别代表正 $n$ 边形的顶点。有一个蓝色钉子在正 $n$ 边形的正中间,如图所示。现在还有一个橡皮筋将 $n$ 个顶点围住,形成一个正 $n$ 边形的轮廓如图所示。
现在有一个空序列 $a$,在橡皮筋没有碰到蓝色钉子之前你可以执行以下操作:
- 选择一个编号为 $x$ 的钉子并且这个钉子并没有被消除。
- 将这个钉子给消除并且将 $x$ 加入到 $a$ 中。
你需要计算出最终可以得到多少种不同的 $a$,这个结果很大,你只需要输出它对 $p$ 进行取模的值,保证 $p$ 是一个素数。
**题目描述**
Doremy has $ n+1 $ pegs. There are $ n $ red pegs arranged as vertices of a regular $ n $ -sided polygon, numbered from $ 1 $ to $ n $ in anti-clockwise order. There is also a blue peg of slightly smaller diameter in the middle of the polygon. A rubber band is stretched around the red pegs.
Doremy is very bored today and has decided to play a game. Initially, she has an empty array $ a $ . While the rubber band does not touch the blue peg, she will:
1. choose $ i $ ( $ 1 \leq i \leq n $ ) such that the red peg $ i $ has not been removed;
2. remove the red peg $ i $ ;
3. append $ i $ to the back of $ a $ .
Doremy wonders how many possible different arrays $ a $ can be produced by the following process. Since the answer can be big, you are only required to output it modulo $ p $ . $ p $ is guaranteed to be a prime number.
**输入输出格式**
**输入格式**
第一行包含两个整数 $ n $ 和 $ p $ ( $ 3 \leq n \leq 5000 $ , $ 10^8 \le p \le 10^9 $ ) — 分别是红色钉子的数量和模数。
$ p $ 保证是一个素数。
**输出格式**
输出一个整数,即可以通过上述过程产生的不同数组 $ a $ 的数量对 $ p $ 取模的结果。
**输入输出样例**
**输入样例 #1**
```
4 100000007
```
**输出样例 #1**
```
16
```
**输入样例 #2**
```
1145 141919831
```
**输出样例 #2**
```
105242108
```
**说明**
在第一个测试案例中, $ n=4 $ ,可以产生的一些可能的数组 $ a $ 有 $ [4,2,3] $ 和 $ [1,4] $ 。然而, $ a $ 不可能是 $ [1] $ 或 $ [1,4,3] $ 。**题意翻译** 现在有 $n+1$ 个钉子。有红色钉子 $n$ 个,它们如图所示排列成一个正 $n$ 边形,它们逆时针从 $1$ 到 $n$ 进行标号,它们分别代表正 $n$ 边形的顶点。有一个蓝色钉子在正 $n$ 边形的正中间,如图所示。现在还有一个橡皮筋将 $n$ 个顶点围住,形成一个正 $n$ 边形的轮廓如图所示。 现在有一个空序列 $a$,在橡皮筋没有碰到蓝色钉子之前你可以执行以下操作: - 选择一个编号为 $x$ 的钉子并且这个钉子并没有被消除。 - 将这个钉子给消除并且将 $x$ 加入到 $a$ 中。 你需要计算出最终可以得到多少种不同的 $a$,这个结果很大,你只需要输出它对 $p$ 进行取模的值,保证 $p$ 是一个素数。 **题目描述** Doremy has $ n+1 $ pegs. There are $ n $ red pegs arranged as vertices of a regular $ n $ -sided polygon, numbered from $ 1 $ to $ n $ in anti-clockwise order. There is also a blue peg of slightly smaller diameter in the middle of the polygon. A rubber band is stretched around the red pegs. Doremy is very bored today and has decided to play a game. Initially, she has an empty array $ a $ . While the rubber band does not touch the blue peg, she will: 1. choose $ i $ ( $ 1 \leq i \leq n $ ) such that the red peg $ i $ has not been removed; 2. remove the red peg $ i $ ; 3. append $ i $ to the back of $ a $ . Doremy wonders how many possible different arrays $ a $ can be produced by the following process. Since the answer can be big, you are only required to output it modulo $ p $ . $ p $ is guaranteed to be a prime number. **输入输出格式** **输入格式** 第一行包含两个整数 $ n $ 和 $ p $ ( $ 3 \leq n \leq 5000 $ , $ 10^8 \le p \le 10^9 $ ) — 分别是红色钉子的数量和模数。 $ p $ 保证是一个素数。 **输出格式** 输出一个整数,即可以通过上述过程产生的不同数组 $ a $ 的数量对 $ p $ 取模的结果。 **输入输出样例** **输入样例 #1** ``` 4 100000007 ``` **输出样例 #1** ``` 16 ``` **输入样例 #2** ``` 1145 141919831 ``` **输出样例 #2** ``` 105242108 ``` **说明** 在第一个测试案例中, $ n=4 $ ,可以产生的一些可能的数组 $ a $ 有 $ [4,2,3] $ 和 $ [1,4] $ 。然而, $ a $ 不可能是 $ [1] $ 或 $ [1,4,3] $ 。
现在有 $n+1$ 个钉子。有红色钉子 $n$ 个,它们如图所示排列成一个正 $n$ 边形,它们逆时针从 $1$ 到 $n$ 进行标号,它们分别代表正 $n$ 边形的顶点。有一个蓝色钉子在正 $n$ 边形的正中间,如图所示。现在还有一个橡皮筋将 $n$ 个顶点围住,形成一个正 $n$ 边形的轮廓如图所示。
现在有一个空序列 $a$,在橡皮筋没有碰到蓝色钉子之前你可以执行以下操作:
- 选择一个编号为 $x$ 的钉子并且这个钉子并没有被消除。
- 将这个钉子给消除并且将 $x$ 加入到 $a$ 中。
你需要计算出最终可以得到多少种不同的 $a$,这个结果很大,你只需要输出它对 $p$ 进行取模的值,保证 $p$ 是一个素数。
**题目描述**
Doremy has $ n+1 $ pegs. There are $ n $ red pegs arranged as vertices of a regular $ n $ -sided polygon, numbered from $ 1 $ to $ n $ in anti-clockwise order. There is also a blue peg of slightly smaller diameter in the middle of the polygon. A rubber band is stretched around the red pegs.
Doremy is very bored today and has decided to play a game. Initially, she has an empty array $ a $ . While the rubber band does not touch the blue peg, she will:
1. choose $ i $ ( $ 1 \leq i \leq n $ ) such that the red peg $ i $ has not been removed;
2. remove the red peg $ i $ ;
3. append $ i $ to the back of $ a $ .
Doremy wonders how many possible different arrays $ a $ can be produced by the following process. Since the answer can be big, you are only required to output it modulo $ p $ . $ p $ is guaranteed to be a prime number.
**输入输出格式**
**输入格式**
第一行包含两个整数 $ n $ 和 $ p $ ( $ 3 \leq n \leq 5000 $ , $ 10^8 \le p \le 10^9 $ ) — 分别是红色钉子的数量和模数。
$ p $ 保证是一个素数。
**输出格式**
输出一个整数,即可以通过上述过程产生的不同数组 $ a $ 的数量对 $ p $ 取模的结果。
**输入输出样例**
**输入样例 #1**
```
4 100000007
```
**输出样例 #1**
```
16
```
**输入样例 #2**
```
1145 141919831
```
**输出样例 #2**
```
105242108
```
**说明**
在第一个测试案例中, $ n=4 $ ,可以产生的一些可能的数组 $ a $ 有 $ [4,2,3] $ 和 $ [1,4] $ 。然而, $ a $ 不可能是 $ [1] $ 或 $ [1,4,3] $ 。**题意翻译** 现在有 $n+1$ 个钉子。有红色钉子 $n$ 个,它们如图所示排列成一个正 $n$ 边形,它们逆时针从 $1$ 到 $n$ 进行标号,它们分别代表正 $n$ 边形的顶点。有一个蓝色钉子在正 $n$ 边形的正中间,如图所示。现在还有一个橡皮筋将 $n$ 个顶点围住,形成一个正 $n$ 边形的轮廓如图所示。 现在有一个空序列 $a$,在橡皮筋没有碰到蓝色钉子之前你可以执行以下操作: - 选择一个编号为 $x$ 的钉子并且这个钉子并没有被消除。 - 将这个钉子给消除并且将 $x$ 加入到 $a$ 中。 你需要计算出最终可以得到多少种不同的 $a$,这个结果很大,你只需要输出它对 $p$ 进行取模的值,保证 $p$ 是一个素数。 **题目描述** Doremy has $ n+1 $ pegs. There are $ n $ red pegs arranged as vertices of a regular $ n $ -sided polygon, numbered from $ 1 $ to $ n $ in anti-clockwise order. There is also a blue peg of slightly smaller diameter in the middle of the polygon. A rubber band is stretched around the red pegs. Doremy is very bored today and has decided to play a game. Initially, she has an empty array $ a $ . While the rubber band does not touch the blue peg, she will: 1. choose $ i $ ( $ 1 \leq i \leq n $ ) such that the red peg $ i $ has not been removed; 2. remove the red peg $ i $ ; 3. append $ i $ to the back of $ a $ . Doremy wonders how many possible different arrays $ a $ can be produced by the following process. Since the answer can be big, you are only required to output it modulo $ p $ . $ p $ is guaranteed to be a prime number. **输入输出格式** **输入格式** 第一行包含两个整数 $ n $ 和 $ p $ ( $ 3 \leq n \leq 5000 $ , $ 10^8 \le p \le 10^9 $ ) — 分别是红色钉子的数量和模数。 $ p $ 保证是一个素数。 **输出格式** 输出一个整数,即可以通过上述过程产生的不同数组 $ a $ 的数量对 $ p $ 取模的结果。 **输入输出样例** **输入样例 #1** ``` 4 100000007 ``` **输出样例 #1** ``` 16 ``` **输入样例 #2** ``` 1145 141919831 ``` **输出样例 #2** ``` 105242108 ``` **说明** 在第一个测试案例中, $ n=4 $ ,可以产生的一些可能的数组 $ a $ 有 $ [4,2,3] $ 和 $ [1,4] $ 。然而, $ a $ 不可能是 $ [1] $ 或 $ [1,4,3] $ 。