310800: CF1889E. Doremy's Swapping Trees
Description
Consider two undirected graphs $G_1$ and $G_2$. Every node in $G_1$ and in $G_2$ has a label. Doremy calls $G_1$ and $G_2$ similar if and only if:
- The labels in $G_1$ are distinct, and the labels in $G_2$ are distinct.
- The set $S$ of labels in $G_1$ coincides with the set of labels in $G_2$.
- For every pair of two distinct labels $u$ and $v$ in $S$, the corresponding nodes are in the same connected component in $G_1$ if and only if they are in the same connected component in $G_2$.
Now Doremy gives you two trees $T_1$ and $T_2$ with $n$ nodes, labeled from $1$ to $n$. You can do the following operation any number of times:
- Choose an edge set $E_1$ from $T_1$ and an edge set $E_2$ from $T_2$, such that $\overline{E_1}$ and $\overline{E_2}$ are similar. Here $\overline{E}$ represents the graph which is given by only reserving the edge set $E$ from $T$ (i.e., the edge-induced subgraph). In other words, $\overline{E}$ is obtained from $T$ by removing all edges not included in $E$ and further removing all isolated vertices.
- Swap the edge set $E_1$ in $T_1$ with the edge set $E_2$ in $T_2$.
Now Doremy is wondering how many distinct $T_1$ you can get after any number of operations. Can you help her find the answer? Output the answer modulo $10^9+7$.
InputThe input consists of multiple test cases. The first line contains a single integer $t$ ($1\le t\le 2\cdot 10^4$) — the number of test cases. The description of the test cases follows.
The first line contains an integer $n$ ($2\le n\le 10^5$) — the number of nodes in the trees $T_1$ and $T_2$.
Each of the following $n-1$ lines contain two integers $u,v$ ($1\le u,v\le n$), representing an undirected edge in $T_1$. It is guaranteed these edges form a tree.
Each of the following $n-1$ lines contain two integers $u,v$ ($1\le u,v\le n$), representing an undirected edge in $T_2$. It is guaranteed these edges form a tree.
It is guaranteed that the sum of $n$ does not exceed $2\cdot 10^5$.
OutputFor each test case, you should output a single line with an integer, representing the number of distinct $T_1$ after any number of operations, modulo $10^9+7$.
ExampleInput3 2 1 2 2 1 3 1 3 2 3 2 3 2 1 4 1 2 2 3 3 4 4 2 2 1 1 3Output
1 2 4Note
In the first test case, there is at most one distinct $T_1$ having the only edge $(1,2)$.
In the second test case, you can choose the edge set $\{(1,3),(2,3)\}$ in $T_1$, the edge set $\{(1,2),(2,3)\}$ in $T_2$ and swap them. So $T_1$ can be $1-3-2$ or $1-2-3$.
In the third test case, there are $4$ distinct $T_1$, as the following pictures.
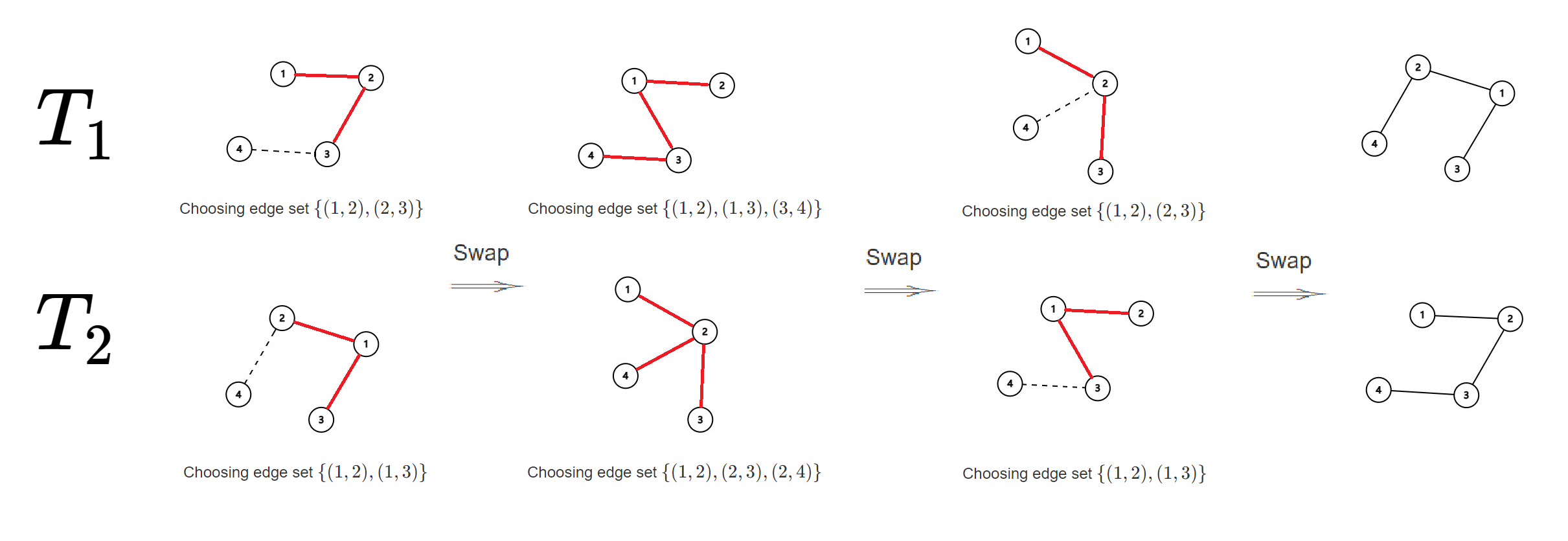
Output
给定两棵树\(T_1\)和\(T_2\),每棵树有\(n\)个节点,节点标号为1到\(n\)。可以进行任意多次以下操作:
1. 从\(T_1\)中选择一个边集\(E_1\),从\(T_2\)中选择一个边集\(E_2\),使得\(\overline{E_1}\)和\(\overline{E_2}\)相似。相似的定义是:\(E_1\)和\(E_2\)的边数相同,且去掉这些边后,剩下的连通块个数相同,每个连通块的大小也相同。
2. 交换\(T_1\)中的边集\(E_1\)和\(T_2\)中的边集\(E_2\)。
问经过任意多次操作后,\(T_1\)有多少种可能的结构。输出答案对\(10^9+7\)取模。
输入数据格式:
第一行包含一个整数\(t\),表示测试用例的数量。
每个测试用例的第一行包含一个整数\(n\),表示\(T_1\)和\(T_2\)的节点数。
接下来\(n-1\)行,每行包含两个整数\(u, v\),表示\(T_1\)的一条边。
再接下来\(n-1\)行,每行包含两个整数\(u, v\),表示\(T_2\)的一条边。
输出数据格式:
对于每个测试用例,输出一行,包含一个整数,表示经过任意多次操作后,\(T_1\)的可能结构数,对\(10^9+7\)取模。题目大意: 给定两棵树\(T_1\)和\(T_2\),每棵树有\(n\)个节点,节点标号为1到\(n\)。可以进行任意多次以下操作: 1. 从\(T_1\)中选择一个边集\(E_1\),从\(T_2\)中选择一个边集\(E_2\),使得\(\overline{E_1}\)和\(\overline{E_2}\)相似。相似的定义是:\(E_1\)和\(E_2\)的边数相同,且去掉这些边后,剩下的连通块个数相同,每个连通块的大小也相同。 2. 交换\(T_1\)中的边集\(E_1\)和\(T_2\)中的边集\(E_2\)。 问经过任意多次操作后,\(T_1\)有多少种可能的结构。输出答案对\(10^9+7\)取模。 输入数据格式: 第一行包含一个整数\(t\),表示测试用例的数量。 每个测试用例的第一行包含一个整数\(n\),表示\(T_1\)和\(T_2\)的节点数。 接下来\(n-1\)行,每行包含两个整数\(u, v\),表示\(T_1\)的一条边。 再接下来\(n-1\)行,每行包含两个整数\(u, v\),表示\(T_2\)的一条边。 输出数据格式: 对于每个测试用例,输出一行,包含一个整数,表示经过任意多次操作后,\(T_1\)的可能结构数,对\(10^9+7\)取模。