405669: GYM102028 J Carpets Removal

Mike's living room is covered by $$$m^2$$$ square tiles. These tiles form a $$$m \times m$$$ grid in which rows are numbered with $$$1$$$ through $$$m$$$ from top to bottom and columns are numbered with $$$1$$$ through $$$m$$$ from left to right.

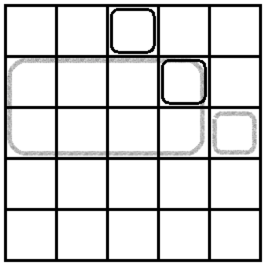
Above these tiles on the floor are laying $$$n$$$ rectangular carpets whose sides are parallel to sides of the grid. Each carpet covers the intersection of several consecutive rows and several consecutive columns, forming a rectangle. Precisely speaking, the $$$i$$$-th carpet of them is described by four integers $$$x_l, x_r, y_l, y_r$$$ with $$$1 \leq x_l \leq x_r \leq m$$$ and $$$1 \leq y_l \leq y_r \leq m$$$, indicating that the carpet covers all tiles which are both ranged from the $$$x_l$$$-th row to the $$$x_r$$$-th row and ranged from the $$$y_l$$$-th column to the $$$y_r$$$-th column.

Now Mike asks you to take away exactly two carpets of them, in order to minimize the number of tiles that would still be covered by at least one remaining carpet.

The figure provided above describes the sample case, in which those two rectangular regions with imaginary boundaries indicate an optimal removal of two carpets.

The input contains several test cases, and the first line contains a positive integer $$$T$$$ indicating the number of test cases which is up to $$$1000$$$.

For each test case, the first line contains two integers $$$n$$$ and $$$m$$$ indicating the number of carpets and the number of tiles in each row or column, where $$$3 \leq n \leq 3 \times 10^5$$$ and $$$1 \leq m \leq 1500$$$.

Each of the following $$$n$$$ lines contains four integers $$$x_l$$$, $$$x_r$$$, $$$y_l$$$, $$$y_r$$$ describing a carpet laying on the floor and its postion, where $$$1 \leq x_l \leq x_r \leq m$$$ and $$$1 \leq y_l \leq y_r \leq m$$$.

We guarantee that the sum of $$$n$$$ in all test cases is up to $$$2 \times 10^6$$$, while the sum of $$$m^2$$$ in all test cases is up to $$$5 \times 10^7$$$.

For each test case, output a line containing the minimum number of tiles that would still be covered by at least one remaining carpet after removal of two carpets.

1
4 5
1 1 3 3
2 2 4 4
3 3 5 5
2 3 1 4

2