405670: GYM102028 K Counting Failures on a Trie

In computer science, a trie, also called prefix tree, is a kind of search tree, an ordered tree data structure, where the keys are usually strings.

Here we have a trie with $$$(n + 1)$$$ nodes labelled $$$0$$$ through $$$n$$$, and its root is the node labelled by $$$0$$$. All edges in the trie are directed from nodes with lower heights to nodes with higher heights. Each of them contains only a lowercase letter, and any two edges with a common starting node have different characters.

We would like to introduce a special matching on the trie for an arbitrary string $$$T[1..k]$$$.

The matching will start at the root, consider all characters $$$T[1], T[2], \cdots, T[k]$$$ in order, and move along some edge which starts from the current node and contains the currently considered character. If the matching arrives at some node but fails to move along some edge, then:

• it will record a failure at the current character, skip the character and move back to the root; and
• it will consider the next character in the next match step because failed characters should be skipped.

Finally, after considering all characters in $$$T$$$, the matching will stay at a node indicating the destination of the matching on the trie. We denote the label of the destination as $$$Dest(T)$$$, and the total number of failures during the matching process as $$$CFail(T)$$$.

Now we give you a string with lowercase letters of length $$$m$$$ denoted by $$$S[1..m]$$$, and you need to answer $$$q$$$ queries. A query is defined as

$$$$$$Query(l, r) = (CFail(S[l..r]), Dest(S[l..r])),$$$$$$

which asks the total number of failures and the destination of the matching for $$$S[l..r]$$$, a substring of $$$S$$$.

The input contains several test cases, and the first line contains a positive integer $$$T$$$ indicating the number of test cases which is up to $$$1000$$$.

For each test case, the first line contains three integers $$$n$$$, $$$m$$$ and $$$q$$$ indicating the number of nodes in the trie, the length of given string $$$S$$$ and the total number of queries respectively, where $$$1 \leq n, m, q \leq 10^5$$$.

The following $$$n$$$ lines describe the trie. The $$$i$$$-th line of them contains an integer $$$f_i$$$, satisfying $$$0 \leq f_i < i$$$, and a lowercase letter $$$c_i$$$ describing the parent node of the $$$i$$$-th node and the character of the edge between them respectively.

The next line contains a string in all lowercase letters indicating the given string $$$S$$$ of length $$$m$$$.

Each of the following $$$q$$$ lines contains two integers $$$l$$$ and $$$r$$$ indicating a query $$$Query(l, r)$$$, where $$$1 \leq l \leq r \leq m$$$.

We guarantee that the sum of $$$n$$$, the sum of $$$m$$$ and the sum of $$$q$$$ in all test cases are up to $$$10^6$$$ respectively.

For each test case, output several lines to answer all queries.

For each query output a line containing two integers in a line indicating $$$CFail(S[l..r])$$$ and $$$Dest(S[l..r])$$$ respectively. You should output exactly one whitespace between these two numbers.

1
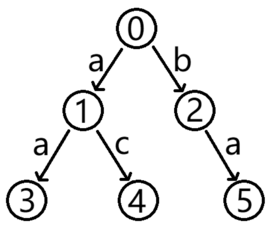
5 10 5
0 a
0 b
1 a
1 c
2 a
aaacbaacab
1 5
1 6
1 7
3 9
4 10

2 2
2 5
3 0
2 1
4 0

The figure below shows the trie given in the sample test case.

Paths for all queries are described as following, where each $$$\Longrightarrow$$$ indicates a failure.

• $$$Path(1, 5) = Path(\unicode{x201C}\texttt{aaacb}\unicode{x201D}) = 0 \longrightarrow 1 \longrightarrow 3 \Longrightarrow 0 \Longrightarrow 0 \longrightarrow 2;$$$
• $$$Path(1, 6) = Path(\unicode{x201C}\texttt{aaacba}\unicode{x201D}) = 0 \longrightarrow 1 \longrightarrow 3 \Longrightarrow 0 \Longrightarrow 0 \longrightarrow 2 \longrightarrow 5;$$$
• $$$Path(1, 7) = Path(\unicode{x201C}\texttt{aaacbaa}\unicode{x201D}) = 0 \longrightarrow 1 \longrightarrow 3 \Longrightarrow 0 \Longrightarrow 0 \longrightarrow 2 \longrightarrow 5 \Longrightarrow 0;$$$
• $$$Path(3, 9) = Path(\unicode{x201C}\texttt{acbaaca}\unicode{x201D}) = 0 \longrightarrow 1 \longrightarrow 4 \Longrightarrow 0 \longrightarrow 1 \longrightarrow 3 \Longrightarrow 0 \longrightarrow 1;$$$
• $$$Path(4, 10) = Path(\unicode{x201C}\texttt{cbaacab}\unicode{x201D}) = 0 \Longrightarrow 0 \longrightarrow 2 \longrightarrow 5 \Longrightarrow 0 \Longrightarrow 0 \longrightarrow 1 \Longrightarrow 0.$$$