407686: GYM102873 F Game on Grid

Alice and Bob are playing a game on an $$$n\times n$$$ grid made of square cells. They play a game and each player wants to paint more cells in their color. Initially, all cells have no color.

In one move, Alice can choose a $$$2 \times 2$$$ empty square and paint all four cells red. None of those four cells can be colored before, and they all must be inside the grid. If there is no available $$$2 \times 2$$$ square, Alice must pass and Bob will keep making moves.

In Bob's move, he can paint one empty cell blue.

They move alternately, Alice goes first. The game stops when all cells are painted (so neither of them can make a move).

If they both play optimally, who will have more cells at the end? Print Alice if there will be strictly more red cells than blue cells; Bob for more blue cells; and Draw if there will be same number of blue and red cells.

You have $$$t$$$ test cases to answer.

The first line contains a single integer $$$t$$$ $$$(1 \leq t \leq 1000)$$$, the number of test cases.

The next $$$t$$$ lines contain a single integer $$$n$$$ $$$(1\leq n \leq1000)$$$, the size of the matrix.

For each test case, print one line with the answer Alice, Bob or Draw accordingly.

3
3
1
4

Bob
Bob
Draw

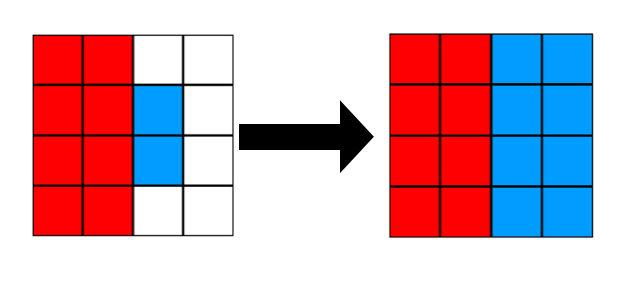
This is a possible situation after two full turns for $$$n = 4$$$. Alice then can't make any more moves and Bob will cover all the remaining cells, resulting in a draw 8:8.