408738: GYM103286 C Рудольф и здоровый образ жизни
Description
Рудольф решил заняться своим здоровьем. Он прочитал, что ходьба очень полезна, и купил фитнес-браслет, чтобы отслеживать свои успехи. В течение $$$N$$$ дней браслет считал, сколько шагов $$$S_i$$$ за $$$i$$$-й день сделал Рудольф.
Через некоторое время ему захотелось визуализировать свой прогресс, и он расположил на координатной плоскости точки $$$(i, S_i)$$$. Взглянув на получившийся график, Рудольф понял, что отдельно взятые точки не очень репрезентативны. Тогда он решил построить прямую по следующим правилам. Для прямой $$$F(X) = AX + B$$$ он ввёл величину ошибки $$$E = \sum\limits_{i=1}^N{(S_i - F(i)) ^ 2}$$$. Очевидно, чем меньше величина ошибки, тем правильнее прямая покажет прогресс Рудольфа. Но порой точки так сильно отличались, что даже оптимальная прямая казалась ему недостаточно удачной. Тогда Рудольф подумал, почему бы не построить несколько прямых. Он решил разбить весь массив имеющихся у него измерений на несколько непрерывных и непересекающихся частей, для каждой из них построить прямую и посчитать суммарную ошибку. Но чтобы не дробить массив слишком сильно, Рудольф ввёл дополнительный штраф $$$C$$$ за каждую отдельную часть. Он получил следующую формулу ошибки для своей системы оценки успехов: $$$M \cdot C + \sum\limits_{i=1}^M{E_i}$$$, где $$$M$$$ — количество частей, на которые разбит массив данных, а $$$E_i$$$ — величина ошибки $$$i$$$-й части. Такая формула полностью устроила Рудольфа. Но минимизировать эту ошибку оказалось непростой задачей, поэтому он просит вас помочь ему с этим.
Входные данныеПервая строка содержит два целых числа $$$N$$$ и $$$C$$$ ($$$1 \le N \le 5000, 1 \le C \le 10 ^ 6$$$) — количество дней, в течение которых велись записи, и штраф за разбиение соответственно.
Вторая строка содержит $$$N$$$ целых чисел $$$S_i$$$ ($$$1 \le S_i \le 10^6$$$) — количество шагов, сделанных Рудольфом в $$$i$$$-й день.
Выходные данныеВыведите одно вещественное число — минимальную суммарную ошибку, которую можно получить по формуле Рудольфа.
Ваш ответ будет засчитан, если относительная или абсолютная погрешность не будет превышать $$$10^{-6}$$$. Формально если $$$a$$$ — ваш ответ, а $$$b$$$ — ответ жюри, то он будет засчитан, если $$$\frac{|a-b|}{max(b,1)} \leq 10^{-6}$$$.
ПримерыВходные данные4 5 2 1 4 3Выходные данные
8.2000000000Входные данные
4 1 2 1 4 3Выходные данные
2.0000000000Примечание
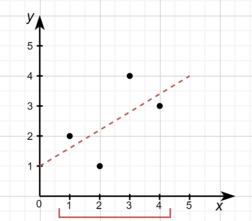
В первом примере оптимальный ответ достигается, если провести одну прямую $$$y = 0.6x + 1$$$ через все точки.
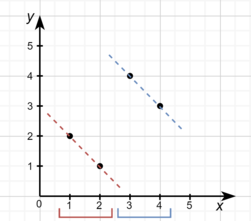
Во втором примере оптимально будет разбить массив точек на две части по две точки.