409399: GYM103496 L Laser Circus

Bob had been invited by Alice and Cindy to attend an anime convention with them, and he's quite excited for the chance to cosplay. He heard that Alice and Cindy will be dressing up as Naruto characters with Kekkei Genkai (Bloodline Limits)—Alice will cosplay as Pakura of the Scorch Release, while Cindy will crossplay as the Sandaime Kazekage (user of Magnet Release). Sticking with this theme, Bob decides to cosplay as Darui, from the Village Hidden in the Clouds! Darui's Bloodline Limit, the Ranton (Storm Release, 嵐遁), allows him to fire laser-like beams of electricity that flow like water. One of his signature jutsus is Laser Circus (励挫鎖苛素­), allowing him to fire multiple beams at once with pinpoint accuracy.

Unfortunately, Bob doesn't actually have the Ranton Bloodline Limit. All he has is a laser pointer. He is also not able to directly manipulate the trajectory of his laser beam, so instead he has set up an elaborate maze of mirrors.

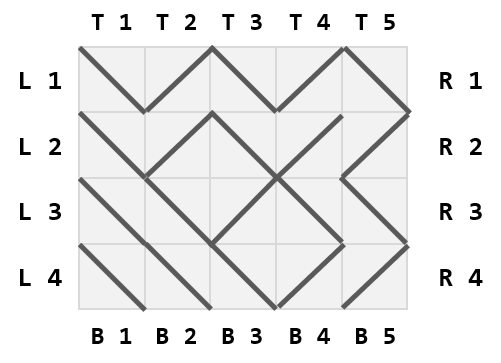
The maze can be seen as a grid with $$$r$$$ rows and $$$c$$$ columns. The left and right boundaries of the rows are labeled L and R, while the top and bottom boundaries of the columns are labeled T and B. The rows are numbered $$$1$$$ to $$$r$$$ from top to bottom, and the columns are numbered $$$1$$$ to $$$c$$$ from left to right. Each boundary edge of the maze can be described by its label and row/column number. Each square in the grid contains a single double-sided mirror oriented at a $$$45^{\circ}$$$ angle, connecting two opposite corners of that square. Please refer to this illustration of the maze from the second sample input, as an example of how the labeling scheme works.

Bob will be firing his laser into the maze from one of its boundary edges (at an angle perpendicular to that edge). When the laser hits a mirror, it reflects off it at a 90 degree angle and keeps bouncing around in the maze until it leaves. Bob wants you to determine where the laser will exit the maze.

Also, he will be firing his laser into the maze $$$q$$$ different times, each from a different starting location. Find the exit location of the laser in each of these occurrences.

The first line of input contains two space-separated integers $$$r$$$ and $$$c$$$, the number of rows and the number of columns in the maze.

Then, $$$r$$$ lines follow, each containing a string with $$$c$$$ characters. This encodes the maze. Each character is either \, representing a mirror that connects the top left and bottom right corners, or /, representing a mirror that connects the top right and bottom left corners.

The next line of input contains a single integer $$$q$$$, the number of queries.

Then, $$$q$$$ lines follow, each describing a query. Each line contains the boundary edge from which Bob was firing her laser into the maze, described by its label and row/column number, with a space separating the two.

Contestants are recommended to use fast methods of input and output for this problem.

For each query, output a line containing the label and row/column number (separated by a space) of the boundary edge from which the laser will exit the maze.

$$$$$$\begin{align*}

&\begin{array}{|l|} \hline \text{Constraints For All Subtasks} \\ \hline 1 \leq r \times c \leq 10^5 \\ 1 \leq q \leq \min(2(r+c),10^5) \\ \text{No two queries begin at the same starting location.} \\ \hline \end{array}\\

&\begin{array}{|c|c|l|} \hline \text{Subtask} & \text{Points} & \text{Constraints} \\ \hline 1 & \mathbf{30} & \text{All mirrors are oriented like }\mathtt{/}\text{} \\ \hline 2 & \mathbf{20} & r = 1 \\ \hline 3 & \mathbf{20} & \text{$r\times c \leq 10^3$} \\ \hline 4 & \mathbf{30} & \text{No further constraints.} \\ \hline \end{array}\\

\end{align*}$$$$$$

1 1
/
4
R 1
L 1
T 1
B 1

B 1
T 1
L 1
R 1

4 5
\/\/\
\/\//
\\/\\
\\\//
4
T 2
R 1
L 3
B 4

T 1
T 5
B 2
L 1

Recall that you need to use an escape sequence to use the backslash character literal in most programming languages.

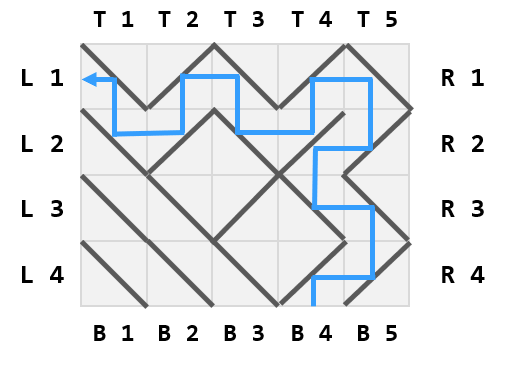
Let's look at each of the queries from the second sample input. This is the path of the laser when fired from the top of the $$$2$$$nd column.

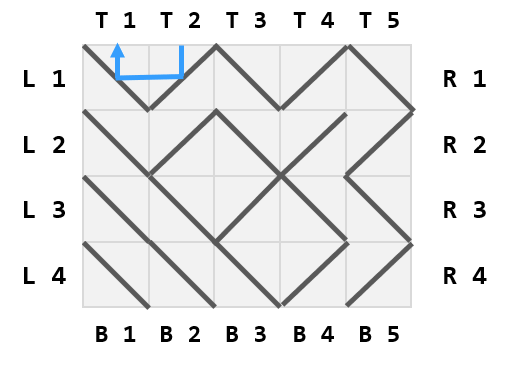
This is the path of the laser when fired from the right of the $$$1$$$st row.

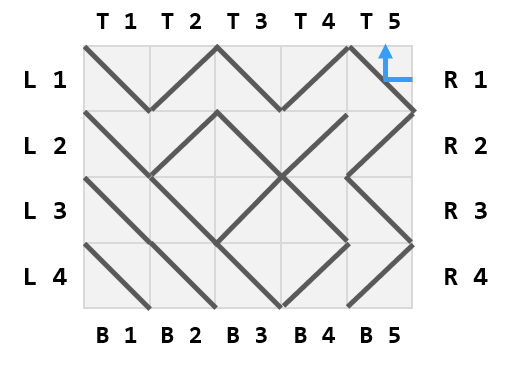
This is the path of the laser when fired from the left of the $$$3$$$rd row.

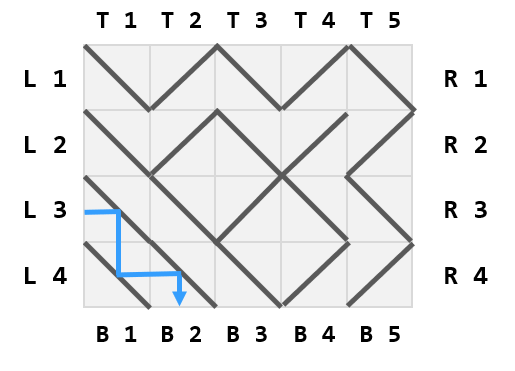
This is the path of the laser when fired from the bottom of the $$$4$$$th column.