Number of Groups

题意翻译

给定 $n$ 条有色线段，每条线段不是红色就是蓝色。一条线段可以被表示为 $(c_i,l_i,r_i)$，其中 $c_i$ 表示线段的颜色，$0$ 代表红色，$1$ 代表蓝色；$l_i,r_i$ 分别表示线段的左右端点。 如果两条异色线段有公共点，那么在这两条线段之间连一条边；多组数据，询问给定 $n$ 条有色线段构成连通块的个数。

题目描述

You are given $ n $ colored segments on the number line. Each segment is either colored red or blue. The $ i $ -th segment can be represented by a tuple $ (c_i, l_i, r_i) $ . The segment contains all the points in the range $ [l_i, r_i] $ , inclusive, and its color denoted by $ c_i $ : - if $ c_i = 0 $ , it is a red segment; - if $ c_i = 1 $ , it is a blue segment. We say that two segments of different colors are connected, if they share at least one common point. Two segments belong to the same group, if they are either connected directly, or through a sequence of directly connected segments. Find the number of groups of segments.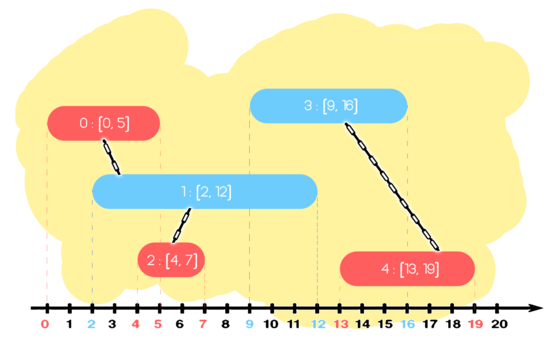 

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^5 $ ). Description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 1 \leq n \leq 10^5 $ ) — the number of segments. Each of the next $ n $ lines contains three integers $ c_i, l_i, r_i $ ( $ 0 \leq c_i \leq 1, 0 \leq l_i \leq r_i \leq 10^9 $ ), describing the $ i $ -th segment. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^5 $ .

输出格式

For each test case, print a single integer $ k $ , the number of groups of segments.

输入输出样例

输入样例 #1

2
5
0 0 5
1 2 12
0 4 7
1 9 16
0 13 19
3
1 0 1
1 1 2
0 3 4

输出样例 #1

2
3

说明

In the first example there are $ 5 $ segments. The segments $ 1 $ and $ 2 $ are connected, because they are of different colors and share a point. Also, the segments $ 2 $ and $ 3 $ are connected, and so are segments $ 4 $ and $ 5 $ . Thus, there are two groups: one containing segments $ \{1, 2, 3\} $ , and the other one containing segments $ \{4, 5\} $ .

题意翻译

给定 $n$ 条有色线段，每条线段不是红色就是蓝色。一条线段可以被表示为 $(c_i,l_i,r_i)$，其中 $c_i$ 表示线段的颜色，$0$ 代表红色，$1$ 代表蓝色；$l_i,r_i$ 分别表示线段的左右端点。 如果两条异色线段有公共点，那么在这两条线段之间连一条边；多组数据，询问给定 $n$ 条有色线段构成连通块的个数。