Ela and the Wiring Wizard

题意翻译

有一个包含 $n$ 个点和 $m$ 条边的无向图，每条边 $i$ 连接着点 $u_i$ 和 $v_i$，权值为 $w_i$，通过这条边要用 $w_i$ 微秒。 Ela 需要从 $1$ 号点走到 $n$ 号点，但他觉得原本的路径太长了。好在，Wiring Wizard 可以帮他改变路径。 具体地，对于任意三点 $u,v,t$（$u$ 和 $t$ 可以相同），若 $u$ 与 $v$ 之间有边 $i$，且 $v$ 与 $t$ 有边 $j$，那么他可以用 $w_i$ 微秒断开边 $i$，并且在 $u$ 与 $t$ 之间连一条权值为 $w_i$ 的边。他可以改任意条边，也可以不改。 Ela 想知道，他至少要花多久时间才能从 $1$ 号点走到 $n$ 号点（时间包括修改边的时间）。 有 $t$ 组数据。 $1\le t\le 100$ $2\le n\le 500\ ,\ n-1\le m\le 250000$ $1\le u_i,v_i\le n\ ,\ 1\le w_i\le 10^9$ $\Sigma{n}\le 500\ ,\ \Sigma{m}\le 250000$ 保证输入的图为联通图，无自环，但可能有重边。

题目描述

Ela needs to send a large package from machine $ 1 $ to machine $ n $ through a network of machines. Currently, with the network condition, she complains that the network is too slow and the package can't arrive in time. Luckily, a Wiring Wizard offered her a helping hand. The network can be represented as an undirected connected graph with $ n $ nodes, each node representing a machine. $ m $ wires are used to connect them. Wire $ i $ is used to connect machines $ u_i $ and $ v_i $ , and has a weight $ w_i $ . The aforementioned large package, if going through wire $ i $ , will move from machine $ u_i $ to machine $ v_i $ (or vice versa) in exactly $ w_i $ microseconds. The Wiring Wizard can use his spell an arbitrary number of times. For each spell, he will choose the wire of index $ i $ , connecting machine $ u_i $ and $ v_i $ , and rewire it following these steps: - Choose one machine that is connected by this wire. Without loss of generality, let's choose $ v_i $ . - Choose a machine that is currently connecting to $ v_i $ (including $ u_i $ ), call it $ t_i $ . Disconnect the wire indexed $ i $ from $ v_i $ , then using it to connect $ u_i $ and $ t_i $ . The rewiring of wire $ i $ will takes $ w_i $ microseconds, and the weight of the wire will not change after this operation. After a rewiring, a machine might have some wire connect it with itself. Also, the Wiring Wizard has warned Ela that rewiring might cause temporary disconnections between some machines, but Ela just ignores it anyway. Her mission is to send the large package from machine $ 1 $ to machine $ n $ as fast as possible. Note that the Wizard can use his spell on a wire zero, one, or many times. To make sure the network works seamlessly while transferring the large package, once the package starts transferring from machine $ 1 $ , the Wiring Wizard cannot use his spell to move wires around anymore. Ela wonders, with the help of the Wiring Wizard, what is the least amount of time needed to transfer the large package from machine $ 1 $ to $ n $ .

输入输出格式

输入格式

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 100 $ ). The description of the test cases follows. The first line contains $ n $ and $ m $ ( $ 2 \le n \le 500 $ , $ n - 1 \le m \le 250 000 $ ), the number of nodes and number of wires, respectively. For the next $ m $ lines, $ i $ -th line will contains $ u_i $ , $ v_i $ and $ w_i $ ( $ 1 \le u_i, v_i \le n $ , $ 1 \le w_i \le 10^9 $ ) - the indices 2 machines that are connected by the $ i $ -th edge and the weight of it. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 500 $ and the sum of $ m $ over all test cases does not exceed $ 250 000 $ . The graph in each test case is guaranteed to be connected, no self-loops, but it can contain multiple edges.

输出格式

For each test case, output one integer denotes the least amount of time needed to transfer the large package from machine $ 1 $ to $ n $ .

输入输出样例

输入样例 #1

3
8 9
1 2 3
6 4 5
3 5 6
6 1 3
7 4 4
3 8 4
2 3 3
7 8 5
4 5 2
4 5
1 2 1
2 4 1
3 4 1
3 1 1
1 3 2
8 8
4 6 92
7 1 65
6 5 43
6 7 96
4 3 74
4 8 54
7 4 99
2 5 22

输出样例 #1

9
2
154

说明

Here is the graph in the first test case in the sample input: 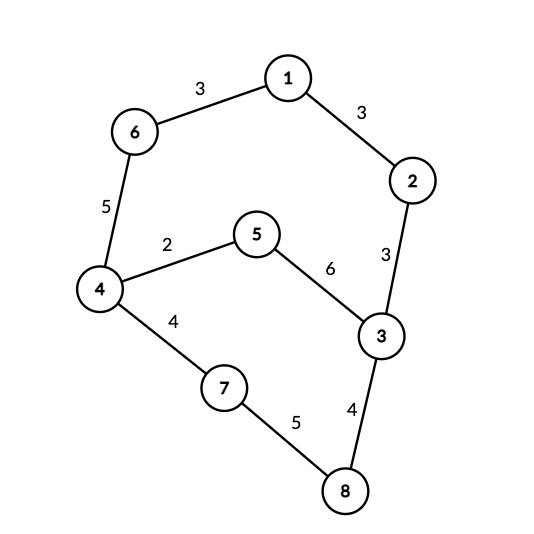Ela can ask the Wiring Wizard to use his spell on wire with the index of $ 7 $ , which is connecting machines $ 2 $ and $ 3 $ . Then, since the machine $ 8 $ is connected to machine $ 3 $ , the Wiring Wizard can disconnect wire $ 7 $ from machine $ 3 $ and connect it to machine $ 8 $ in $ 3 $ microseconds (weight of wire $ 3 $ ). After that, the package can be sent from machine $ 1 $ to machine $ 8 $ in $ 6 $ microseconds. Therefore, the answer is $ 3 + 6 = 9 $ microseconds. Here is the graph in the third test case in the sample 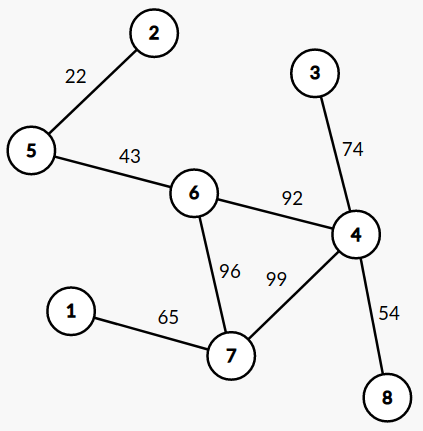input: 

**题意翻译**

题目描述了一个包含 $ n $ 个节点和 $ m $ 条边的无向图。每条边 $ i $ 都连接着两个节点 $ u_i $ 和 $ v_i $，并具有权值 $ w_i $，表示通过这条边需要 $ w_i $ 微秒的时间。Ela 需要从节点 $ 1 $ 走到节点 $ n $，但她认为最短路径太慢。Wiring Wizard 可以帮助她通过改变路径来加速这一过程。

具体来说，对于任意三个节点 $ u, v, t $（其中 $ u $ 和 $ t $ 可以相同），如果 $ u $ 与 $ v $ 之间有边 $ i $，且 $ v $ 与 $ t $ 之间有边 $ j $，那么 Wiring Wizard 可以在 $ w_i $ 微秒内断开边 $ i $，并在 $ u $ 与 $ t $ 之间建立一条具有相同权值 $ w_i $ 的新边。他可以选择对任意数量的边进行修改，也可以选择不修改任何边。

Ela 想知道，在 Wiring Wizard 的帮助下，她至少需要多长时间才能从节点 $ 1 $ 到达节点 $ n $（包括修改边的时间）。保证输入的图是联通的，没有自环，但可能有重边。

**输入输出格式**

**输入格式：**
- 每个测试包含多个测试用例。第一行包含测试用例的数量 $ t $（$ 1 \le t \le 100 $）。
- 每个测试用例的第一行包含两个整数 $ n $ 和 $ m $（$ 2 \le n \le 500 $，$ n - 1 \le m \le 250000 $），分别表示节点的数量和边的数量。
- 接下来的 $ m $ 行，每行包含三个整数 $ u_i $，$ v_i $ 和 $ w_i $（$ 1 \le u_i, v_i \le n $，$ 1 \le w_i \le 10^9 $），分别表示第 $ i $ 条边连接的两个节点的编号和边的权值。
- 保证所有测试用例中 $ n $ 的总和不超过 $ 500 $，$ m $ 的总和不超过 $ 250000 $。每个测试用例的图保证是联通的，没有自环，但可能有重边。

**输出格式：**
- 对于每个测试用例，输出一个整数，表示从节点 $ 1 $ 到节点 $ n $ 传输大包裹所需的最少时间。

**输入输出样例**

**输入样例 #1：**
```
3
8 9
1 2 3
6 4 5
3 5 6
6 1 3
7 4 4
3 8 4
2 3 3
7 8 5
4 5 2
4 5
1 2 1
2 4 1
3 4 1
3 1 1
1 3 2
8 8
4 6 92
7 1 65
6 5 43
6 7 96
4 3 74
4 8 54
7 4 99
2 5 22
```

**输出样例 #1：**
```
9
2
154
```

**说明：**

题目描述了通过重新连接网络中的边来找到从节点 $ 1 $ 到节点 $ n $ 的最短路径。需要注意的是，一旦包裹开始从节点 $ 1 $ 传输，Wiring Wizard 就不能再使用他的咒语来移动边。**题意翻译** 题目描述了一个包含 $ n $ 个节点和 $ m $ 条边的无向图。每条边 $ i $ 都连接着两个节点 $ u_i $ 和 $ v_i $，并具有权值 $ w_i $，表示通过这条边需要 $ w_i $ 微秒的时间。Ela 需要从节点 $ 1 $ 走到节点 $ n $，但她认为最短路径太慢。Wiring Wizard 可以帮助她通过改变路径来加速这一过程。 具体来说，对于任意三个节点 $ u, v, t $（其中 $ u $ 和 $ t $ 可以相同），如果 $ u $ 与 $ v $ 之间有边 $ i $，且 $ v $ 与 $ t $ 之间有边 $ j $，那么 Wiring Wizard 可以在 $ w_i $ 微秒内断开边 $ i $，并在 $ u $ 与 $ t $ 之间建立一条具有相同权值 $ w_i $ 的新边。他可以选择对任意数量的边进行修改，也可以选择不修改任何边。 Ela 想知道，在 Wiring Wizard 的帮助下，她至少需要多长时间才能从节点 $ 1 $ 到达节点 $ n $（包括修改边的时间）。保证输入的图是联通的，没有自环，但可能有重边。 **输入输出格式** **输入格式：** - 每个测试包含多个测试用例。第一行包含测试用例的数量 $ t $（$ 1 \le t \le 100 $）。 - 每个测试用例的第一行包含两个整数 $ n $ 和 $ m $（$ 2 \le n \le 500 $，$ n - 1 \le m \le 250000 $），分别表示节点的数量和边的数量。 - 接下来的 $ m $ 行，每行包含三个整数 $ u_i $，$ v_i $ 和 $ w_i $（$ 1 \le u_i, v_i \le n $，$ 1 \le w_i \le 10^9 $），分别表示第 $ i $ 条边连接的两个节点的编号和边的权值。 - 保证所有测试用例中 $ n $ 的总和不超过 $ 500 $，$ m $ 的总和不超过 $ 250000 $。每个测试用例的图保证是联通的，没有自环，但可能有重边。 **输出格式：** - 对于每个测试用例，输出一个整数，表示从节点 $ 1 $ 到节点 $ n $ 传输大包裹所需的最少时间。 **输入输出样例** **输入样例 #1：** ``` 3 8 9 1 2 3 6 4 5 3 5 6 6 1 3 7 4 4 3 8 4 2 3 3 7 8 5 4 5 2 4 5 1 2 1 2 4 1 3 4 1 3 1 1 1 3 2 8 8 4 6 92 7 1 65 6 5 43 6 7 96 4 3 74 4 8 54 7 4 99 2 5 22 ``` **输出样例 #1：** ``` 9 2 154 ``` **说明：** 题目描述了通过重新连接网络中的边来找到从节点 $ 1 $ 到节点 $ n $ 的最短路径。需要注意的是，一旦包裹开始从节点 $ 1 $ 传输，Wiring Wizard 就不能再使用他的咒语来移动边。